De gemiddelde leerling zal zich uit zijn schoollessen Archimedes vooral herinneren als de naakte man die uit zijn bad sprong terwijl hij Eureka riep, en niet zozeer als wiskundige. Twee eeuwen na zijn dood vond Cicero het graf van Archimedes, en beschreef hij een grafsteen met een reliëftekening van een bol in een cilinder. Dit kan kloppen want van al zijn ontdekkingen was Archimedes het meest trots op zijn formule om het volume van een bol te berekenen. Eigenlijk was hij vooral trots op de methode waarmee hij de volumes van de bol, de kegel en de cilinder wist te vergelijken met elkaar.
De Schorpioen is een uit de kluiten gewassen kruisboog, die door een schutter kan opgespannen worden dankzij een mechanische krachtvermenigvuldiger. Met dit tuig wordt in het laatste seizoen van Game of Thrones een draak van Daenerys Targaryen, uit de lucht geschoten tijdens de belegering van King’s Landing. Dit fantasiefeit greep plaats in 304 n.Chr.
Weinig liefhebbers van deze fantasy reeks weten dat de Scorpio al rond het begin van onze jaartelling door de Romeinen gebruikt werd, en waarschijnlijk zelfs al door het leger van koning Uzzia van Juda in de 8ste eeuw v. Chr.
Maar mij deed dit mechanisch vernuft vooral denken aan de befaamde Griekse wiskundige Archimedes, geboren in Syracuse (287 v.Chr.), waar hij in 212 v.Chr. vermoord werd tijdens de tweede Punische oorlog door een Romeinse soldaat. Volgens de geschiedschrijver Livius gebeurde dit na de irritatie van Archimedes omdat de lompe Romein op een meetkundige figuur stapte die in het zand op de vloer getekend was. Volgens diezelfde Livius waren “Verstoor mijn cirkels niet” de laatste woorden van Archimedes. Soms is wiskunde onverantwoord interessant.
Nochtans had de Romeinse bevelhebber Marcus Marcellus expliciet opgedragen om Archimedes levend gevangen te nemen. In zijn tijd was Archimedes immers een levende legende wegens zijn uitvindingen van werktuigen (zoals de schroefpomp) en militaire toestellen (variaties van de katapult en de schorpioen, de klauw, de zonnespiegels,…). Dankzij deze krijgstuigen kon Syracuse twee jaar standhouden tegen de Romeinse belegering. In de oudheid was hij ook beroemd wegens zijn ontdekkingen van natuurkundige principes in de statica (hefboomregel) en de hydrostatica (opwaartse stuwkracht), terwijl zijn wiskundige inzichten pas eeuwen later en druppelsgewijs tot de wetenschap doordrong. Zijn tijdsgenoten bewonderden Archimedes omdat deze de kroon van de koning van Syracuse in water onderdompelde en hierdoor bewees dat de edelsmid geen zuiver goud gebruikt had.
Maar bijna niemand wist dat hij (als eerste) het getal $\pi$ nauwkeurig kon benaderen, en dat hij de oppervlakte van parabolische gebieden exact kon berekenen, a propos m.b.v. limiet- en integraaltechnieken die pas 2000 jaar nadien werden uitgevonden. Zelfs nu nog zal een gemiddelde leerling uit zijn schoollessen zich Archimedes vooral herinneren als de naakte man die uit zijn bad sprong terwijl hij Eureka riep, en niet zozeer als wiskundige. Twee eeuwen na zijn dood bezocht Cicero de stad Syracuse en ging hij op zoek naar het graf van Archimedes. Behalve de soldaat die zijn voeten veegde aan de bewuste cirkeltekening was ongeveer iedere Romein fan van Archimedes. Naar eigen zeggen heeft Cicero dat graf effectief gevonden. De Romeinse redenaar beschrijft een grafsteen met een reliëftekening van een bol in een cilinder. Dit kan kloppen want van al zijn ontdekkingen was Archimedes het meest trots op zijn formule om het volume van een bol te berekenen. Eigenlijk was hij vooral trots op de methode waarmee hij de volumes van de bol, de kegel en de cilinder wist te vergelijken met elkaar. En deze fierheid was meer dan terecht!
Natuurlijk is mijn associatie tussen de Schorpioen van Game of Thrones en de uitvindingen van Archimedes sterk beïnvloed door een recente vakantietrip naar Syracuse, waar ik minder geluk kende dan Cicero, want het echte graf van Archimedes heb ik niet gevonden, enkel een replica om toeristen te plezieren. Maar ik beveel iedereen aan een bezoek te brengen aan TechnoParco, een soort Archimedes-pretpark.
Wie in dit klein gezellig openluchtmuseum moest aanspoelen, mag zeker niet nalaten om de eigenaar te laten uitpakken met zijn kennis over de Archimedes-puzzel Stomachion.
De bewuste methode van Archimedes is een combinatie van het versnijden van een object in dunne schijfjes (de uitputtingsmethode), gecombineerd met zijn hefboomprincipe. Eigenlijk weten we dit nog maar sinds het begin van vorige eeuw, toen de Deen Johan Ludvig Heiberg in Constantinopel een perkament bestudeerde dat hergebruikt was en dat onder de bovenste lagen een originele brief van Archimedes aan zijn vriend Eratosthenes of Cyrene bevatte.
Laten we eerst het hefboomprincipe in beeld brengen, waarvan Archimedes inderdaad de auteur is. De olifant hieronder weegt 100 000 keer meer dan de muis, maar toch is de wip in evenwicht omdat de muis 100 000 keer verder van het steunpunt F staat dan de olifant. Het product van gewicht en afstand is aan beide kanten van het steunpunt gelijk.
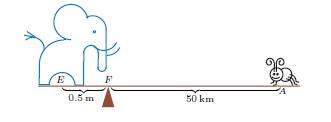
Belangrijk hierbij is dat de afstand tot het steunpunt steeds gemeten wordt vanaf de positie van het zwaartepunt van het voorwerp (muis, olifant of wat dan ook). In zijn bewijsvoering gebruikte Archimedes meestal homogene voorwerpen waarvan hij veronderstelde dat ze alle uit hetzelfde materiaal gemaakt waren (zelfde dichtheid), zodat de verhouding van de gewichten van twee voorwerpen gelijk is aan de verhouding van hun volumes. Dus de evenwichtsvergelijking voor een balans kan geformuleerd worden als $V_1\times d_1 = V_2\times d_2$, voor lichamen met volumes $V_1$ en $V_2$, en met respectieve afstanden $d_1$ en $d_2$ tot het steunpunt.
Dan zijn we nu beland aan de uitputtingsmethode, die met recht mag beschouwd worden als de allereerste integraalcalculus, niettegenstaande de uitvinding van de integraal in de handboeken Analyse meestal toegekend wordt aan Newton of Leibniz (naargelang de auteur de taal van Shakespeare of Goethe spreekt). In de brief die Heiberg aan de oppervlakte bracht, schreef Archimedes de eer voor deze methode geheel toe aan Democritus (460 – 370 v.Chr.). Deze laatste was ook redelijk geniaal te noemen, zodanig zelfs dat een jaloerse Plato ooit voorstelde om al diens geschriften te verbranden. Maar eigenlijk was Archimedes de eerste die nieuwe resultaten behaalde met de uitputtingsmethode.
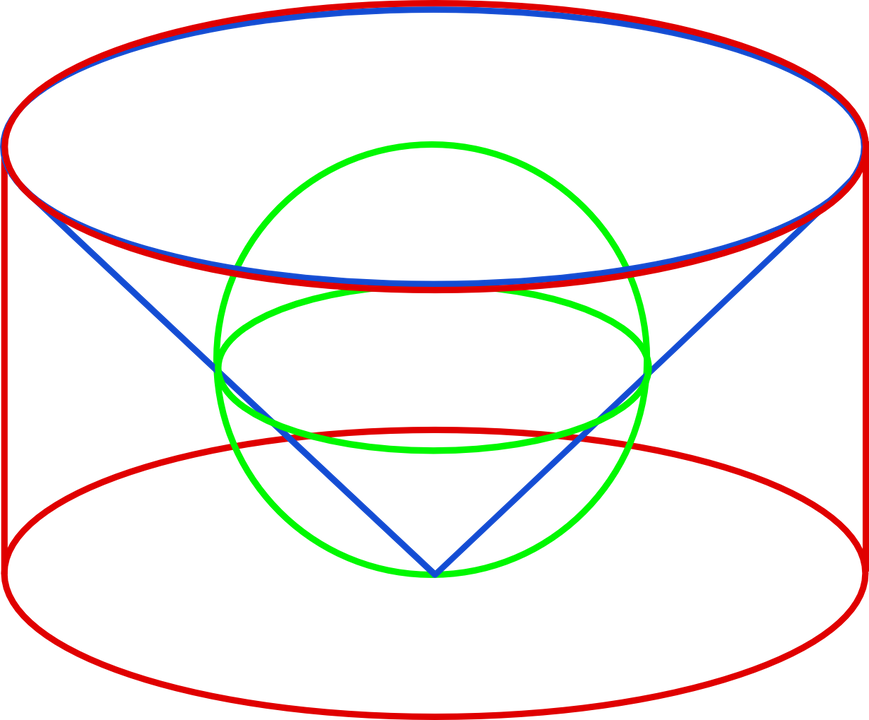
Bereid jullie dan nu voor op een confrontatie met de duizelingwekkende genialiteit waarmee Archimedes de volumes van de bol, de cilinder en de kegel met elkaar wist te vergelijken. Neem een cilinder, een kegel en een bol zoals in onderstaande figuur. We bestuderen de situatie waarbij de straal en de hoogte van de cilinder gelijk zijn aan de diameter van de bol, en waarbij de kegel juist in de cilinder past. Als we $r$ noteren voor de straal van de bol, dan is de straal van de cirkelvormige basis van zowel de kegel als de cilinder gelijk aan $2 r$. Bovendien is de hoogte $h$ van de kegel gelijk aan die van de cilinder en ook gelijk aan de diameter $2 r$ van de bol.
In dit gedachte-experiment wordt de cilinder op zijn kant op een (horizontale) wip gelegd met steunpunt in $A$ (zie figuur). Deze wip kan een as zijn waar de cilinder brochette-gewijs over geschoven is, of gewoon een plank waar de cilinder op ligt, dat doet niets ter zake.
Belangrijk is dat de cirkelvormige doorsneden van de cilinder loodrecht op de wip staan, met het grondvlak op het steunpunt $A$. Het bovenvlak bevindt zich in positie $C$ van de wip op een afstand $2 r$ van $A$, omdat de hoogte van de cilinder gelijk is aan de diameter van de bol. In gedachte plaatsen we de kegel in deze cilinder (wat juist lukt, en op slechts 1 manier), en ook de bol verbeelden we in de cilinder, zodanig dat de cilinder-as ( $=$ kegelas) samenvalt met een diameter van de bol. Gelukkig is dit een gedachte-experiment want praktisch gezien is het onmogelijk om kegel en bol tegelijkertijd in de cilinder te wringen.
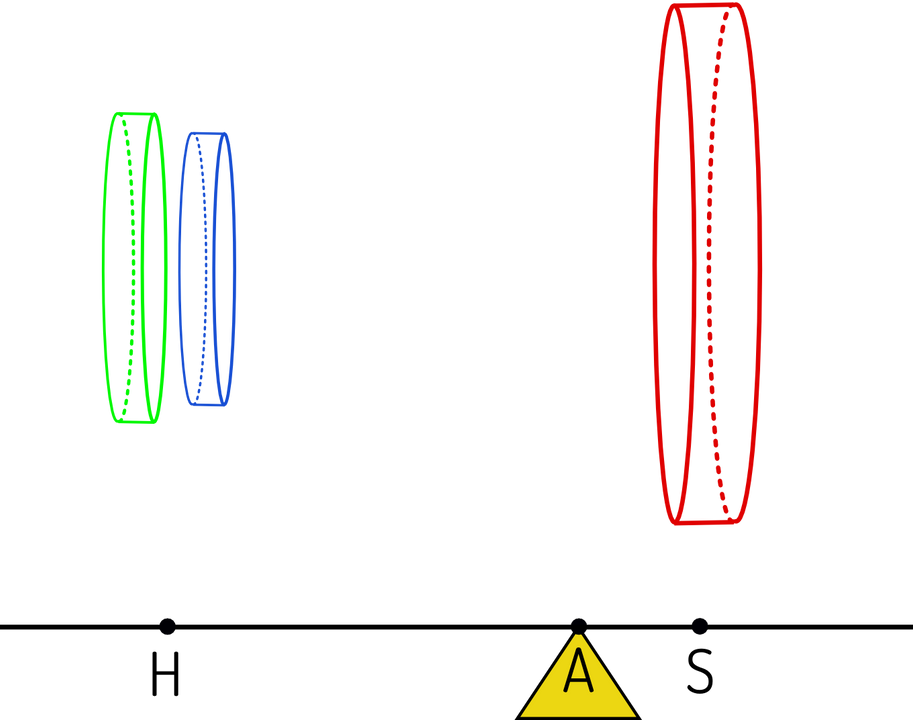
Nu treedt de uitputtingsmethode in werking, waarbij Archimedes deze drie objecten in dunne schijfjes versnijdt, loodrecht op de cilinder-as, van links naar rechts (van $A$ naar $C$ dus). Op ieder moment snijden we simultaan 3 schijfjes uit onze objecten: een cilinderschijf, een bolschijf en een kegelschijf. Deze schijfjes moeten we ons visualiseren als de stenen van een sjoelbak (zie figuur), en zijn dus zelf cilindervormig, weliswaar erg plat, met een kleine hoogte ($=$ dikte van de schijf). Strikt genomen heeft enkel de cilinderschijf een rand loodrecht op het snijvlak, terwijl de rand van een kegelschijf schuin is en die van een bolschijf gebogen, maar als we onze schijfjes voldoende dun snijden zijn deze afwijkingen te verwaarlozen.
De moderne mens heeft noties van het limietbegrip en van infinitesimalen, maar in die tijd was het een hele krachttoer om met schijfjes te werken waarvan de dikte oneindig klein is maar toch niet nul. Ze hebben dus een volume, zoals de sjoelschijven, namelijk de oppervlakte van het cirkelvormige snijvlak vermenigvuldigd met de (infinitesimale) dikte $\delta$. De formule voor de oppervlakte van een cirkel was trouwens gekend door Archimedes (en bewezen!), zijnde $\pi$ maal het kwadraat van de straal.
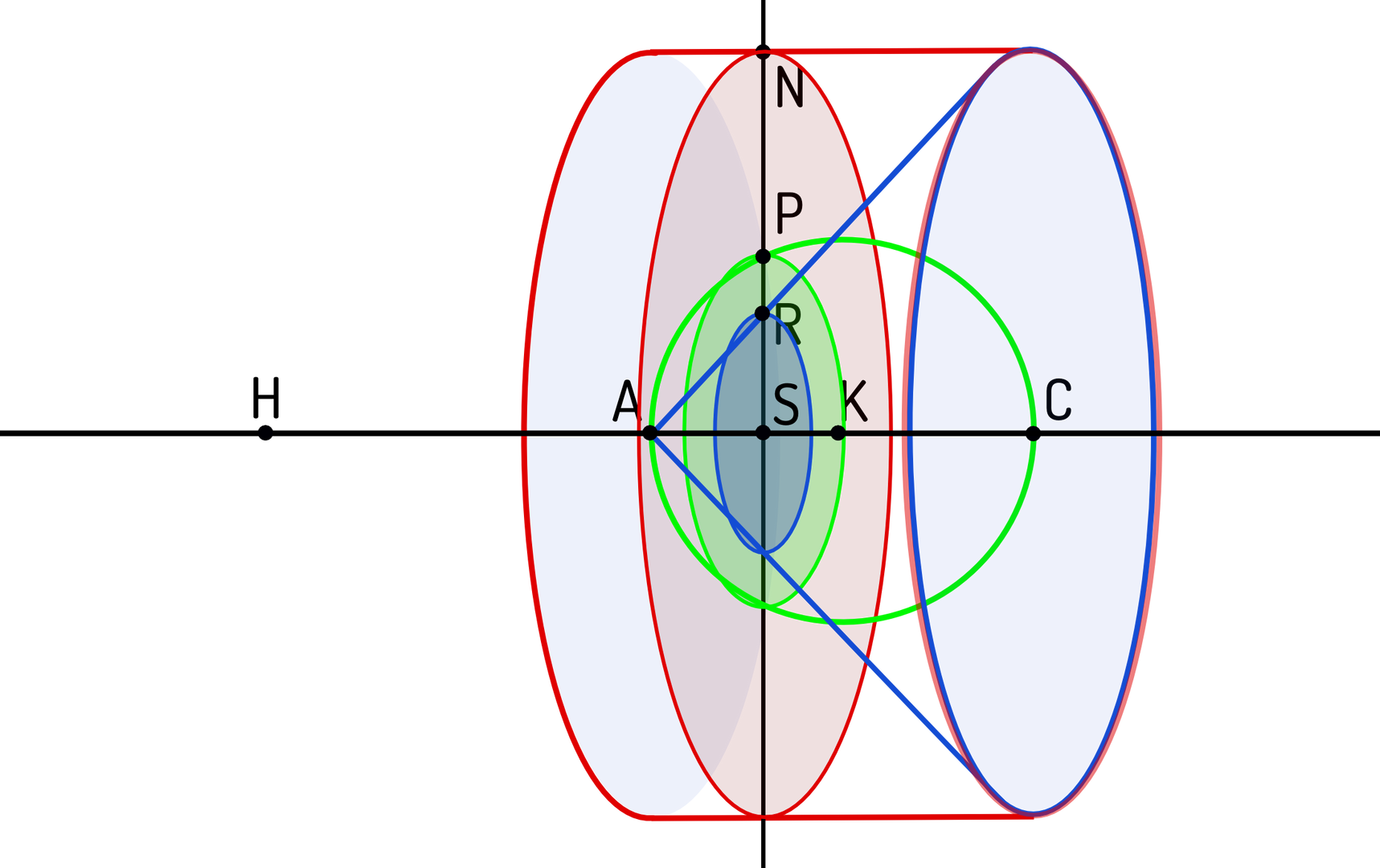
Stel dat onze snijmachine zich in positie $S$ bevindt, op afstand $x$ van het steunpunt $A$ (zie figuur). De 3 schijfjes die we simultaan uitsnijden hebben uiteraard verschillende stralen:
- De cilinderschijf is in iedere snijpositie even groot, met een schijfstraal gelijk aan $2 r$ (de straal van de grote cilinder).
- De straal $|SR|$ van de kegelschijf neemt toe volgens een constante helling van $100\%$ omdat de hoogte van de kegel ($|AC| = 2 r$) juist gelijk is aan de straal van zijn grondvlak. Dus in snijpositie $S$ met $|AS| = x$ is de straal van de kegelschijf ook gelijk aan $x$.
- Om de straal $|SP|$ van de bolschijf te bepalen, gebruiken we de stelling van Pythagoras in het vlak door het middelpunt van de bol en loodrecht op het snijvlak. Hier zien we een rechthoekige driehoek $SKP$ (zie figuur). In snijpositie $x$ is het kwadraat van de bolschijfstraal dus gelijk aan $|KP|^2 - |SK|^2 = r^2 – (r-x)^2 = 2rx – x^2$.
Nu had Archimedes het inzicht dat de cilinderschijf in om het even welke snijpositie $S$ in evenwicht gehouden wordt als we de twee andere schijven (zoals uitgesneden op plaats $S$) in het punt $H$ plaatsen, waarbij dit punt $H$ op een afstand $2r$ ligt van het steunpunt $A$.
De plaats $S$ varieert weliswaar van $A$ tot $C$, terwijl het punt $H$ vastligt, maar de kegel- en bolschijf worden natuurlijk alsmaar groter. Misschien heeft de lezer problemen met het plaatsen van twee schijven in 1 minuscuul punt, maar we bedoelen dat het zwaartepunt van beide schijven zich ter hoogte van $H$ moet bevinden. Het evenwicht volgt uit de berekening van de verhouding van beide volumes (rechts op links):
$$\frac{V_1}{V_2} = \frac{\mbox{vol(cilinderschijf)}}{\mbox{vol(kegelschijf)}+\mbox{ vol(bolschijf)}}$$
Omdat deze 3 schijven dezelfde (infinitesimale) dikte $\delta$ hebben, kan de verhouding $V_1/V_2$ beschouwd worden als de verhouding van de oppervlaktes van de cirkelvormige doorsneden. Omdat $\pi$ een gemeenschappelijke factor is, kunnen we ons zelfs beperken tot de kwadraten van de stralen in de berekening van deze verhouding:
$$\frac{V_1}{V_2} = \frac{4 r^2}{x^2 + (2rx – x^2)}=\frac{4 r^2}{2rx}=\frac{2 r}{x},$$
welke identiek is aan de verhouding van de afstanden zwaartepunt-steunpunt (links op rechts):
$$\frac{d_2}{d_1} = \frac{2r}{x},$$
zodat we in iedere snijpositie $S$ een evenwicht hebben volgens het hefboomprincipe.
De conclusie van de uitputtingsmethode is dat een globaal evenwicht volgt uit de lokale evenwichten per schijfje. Met andere woorden:
De cilinder, helemaal versneden (uitgeput) zoals hij daar ligt tussen $A$ en $C$, wordt t.o.v. het steunpunt $A$ in evenwicht gehouden door de kegel en de bol zoals links gereconstrueerd in het punt $H$.
Het speelt geen rol hoe de kegel en de bol juist geplaatst zijn, zolang hun gezamenlijk zwaartepunt zich ter hoogte van het punt $H$ bevindt. Anderzijds, wegens symmetrie, bevindt het zwaartepunt van de cilinder zich juist in het midden van de cilinder, wat overeenkomt met positie $r$ op de wip. Dit globaal evenwicht betekent dus dat
$$\left({\mbox{vol(kegel)} + \mbox{vol(bol)}}\right)\cdot 2r = \mbox{vol(cilinder)}\cdot r$$
of
$$\mbox{vol(bol)} = \frac{1}{2} \left({\mbox{vol(cilinder)} – 2\cdot\mbox{vol(kegel)}}\right)$$
Nu wist Archimedes dat het volume van een kegel juist een derde is van het volume van de cilinder met dezelfde hoogte en grondvlak als de kegel. Dit staat bijvoorbeeld als Propositie 10 in boek XII van het boek van Euclides. Uit ons kegel-bol-cilinder evenwicht volgt dus dat het volume van een bol $1/6$ is van het volume van de cilinder met hoogte en straal gelijk aan de diameter van de bol. Het volume van dergelijke cilinder (hoogte $=$ straal $= 2r$) is gelijk aan $8 \pi r^3$, en dus dat van de bol $\frac{4}{3}\pi r^3$.
Voor hedendaagse studenten is het een standaardoefening in integraalrekening om deze inhoudsformule af te leiden, maar de prestatie van Archimedes zal altijd van een hogere orde blijven, omdat hij de inhouden van bol, kegel en cilinder rechtstreeks met elkaar in relatie bracht. Het resultaat van Archimedes is bovendien een meer pure vorm van meten, omdat hij geen maattheorie of integraalconstructies gebruikt!
