De eeuwige kopzorgen van een schrikkeldag

Naar schatting iets meer dan 5 miljoen mensen vieren vandaag eindelijk nog eens hun échte verjaardag (zo ook Superman, als in, het fictieve personage, niet de acteur).

Doorheen de geschiedenis werden immers verschillende kalendersystemen gebruikt, die dan dikwijls ook nog eens verschilden van volk tot volk. De oude Romeinse kalender (wat in feite een Romeinse versie van de Egyptische kalender was, in gebruik sinds 713 v.Chr.) was bijvoorbeeld gebaseerd op de maanstanden, en telde 12 maanden met in totaal 355 dagen, onderverdeeld in weken van 8 dagen. Maar de seizoenen zijn afhankelijk van de positie van de aarde in de cyclus rond de zon, en tegen de tijd dat Julius Caesar aan de macht kwam, was de discrepantie tussen de seizoenen en de oude maankalender zo groot geworden dat hij in 45 v.Chr. besloot de kalender te hervormen waarbij hij zich zou baseren op de zon. Ter compensatie van de opgelopen verschillen had het jaar 46 v.Chr. maar liefst 445 dagen verdeeld over 15 maanden.

Bij de hervorming kreeg Caesar de raad van astronoom Sosigenes om elke vier jaar een extra dag toe te voegen, aangezien de exacte omlooptijd van de aarde rond de zon ongeveer 365,25 dagen bedraagt. Maar ook dit is eigenlijk niet correct genoeg, aangezien een juliaans kalenderjaar zo gemiddeld gezien elf minuten langer duurt dan het tropisch jaar. Op een periode van 1000 jaar zou dit verschil oplopen tot zo'n 7,8 dagen. Dit werd door paus Gregorius XIII verholpen in 1582 bij de invoering van de gregoriaanse kalender, het systeem dat vandaag de dag algemeen gebruikt wordt in de westerse wereld. Opnieuw werd eenmalig de opgelopen achterstand gecorrigeerd, waarbij men besloot om 10 dagen over te slaan zodat het begin van de lente terug zou vallen op 21 maart: na donderdag 4 oktober 1582 kwam vrijdag 15 oktober 1582.

Terzelfdertijd werd beslist om per 400 jaar 3 schrikkeldagen te laten vallen: jaartallen die deelbaar zijn door 4 waren reeds schrikkeljaren, maar sinds de gregoriaanse kalender zijn eeuwjaren (jaren die deelbaar zijn door 100) géén schrikkeljaar meer, tenzij ze toch deelbaar zijn door 400. Eigenlijk is ook dit nog niet helemaal correct, want een tropisch jaar duurt eigenlijk net ietsje minder lang dan 365,25 dagen. Het jaar 2000 bijvoorbeeld duurde exact 365 dagen, 5 uur, 48 minuten en 45,18 seconden, ofwel 365,2421896 dagen. Dit verschil loopt op tot ongeveer 1 dag per 3200 jaar. De gregoriaanse kalender schrijft niet voor hoe dit verschil zal moeten worden gecompenseerd, maar dat zijn zorgen voor later.

Als u trouwens dacht dat de overgang naar de gregoriaanse kalender in 1582 zonder slag of stoot verliep, hebt u het ook grondig mis. Enkele rooms-katholieke landen volgden onmiddellijk het pauselijk besluit, maar andere katholieke landen maakten de overgang pas enkele jaren later. Veel protestantse landen en gebieden sloten pas aan rond 1700. In Rusland duurde het zelfs tot 1918, waardoor het verschil tussen de kalenders al opgelopen was tot 13 dagen, zodat na 31 januari onmiddellijk 14 februari volgde. Opmerkelijk hierbij is dat 3 maanden eerder (op 25 oktober 1917 juliaans) de Oktoberrevolutie plaats vond, en dat de eerste herdenking hiervan een jaar later bijgevolg niet meer in oktober maar in november viel. Vandaag de dag wordt de gregoriaanse kalender bijna overal ter wereld gebruikt (groen op de kaart hieronder). Enkel in Afghanistan, Ethiopië, Iran en Nepal (rood) gebruikt men nog een ander kalendersysteem. In Japan, Noord-Korea, Sri Lanka en Thailand (blauw) gebruikt men een aangepaste versie van de gregoriaanse kalender, en in verschillende Arabische en Zuid-Aziatische landen (oranje) gebruikt men naast de gregoriaanse nog een ander soort kalender tegelijkertijd. Op 1 oktober 2016 was Saoedi-Arabië het tot op vandaag laatste land om over te schakelen van de islamitische naar de gregoriaanse kalender.

Even terug naar de juliaanse kalender. Zoals gezegd had deze het relatief eenvoudige systeem om een maal per vier jaar een extra dag in te voeren. Aangezien er zeven dagen in de week zijn, en er twee soorten jaren bestaan (gewone jaren en schrikkeljaren), zijn er 7*2=14 mogelijke kalenders wat betreft dagen van de week in combinatie met datums. Maar zit er ook een vast stramien in de volgorde waarin deze verschillende kalenders voorkomen? Een jaar van 365 dagen bestaat uit exact 52 weken van 7 dagen plus nog een extra dag (365 = 7*52 + 1). Een vaste datum, bijvoorbeeld 1 januari, zal een jaar later dus juist een dag in de week verschuiven. Was deze eerst een dinsdag, dan zal dit een 365-dagen-jaar later een woensdag zijn. Een schrikkeljaar van 366 dagen telt natuurlijk nog een dag extra, en dus zal de verschuiving daar twee dagen zijn. Op een periode van vier jaar, zijnde drie gewone jaren plus een schrikkeljaar, verschuift de vaste datum dus 5 dagen in totaal. Na 2 periodes is dit 10 dagen, na 3 periodes 15 dagen, enzovoort. Na 7 dergelijke periodes zijn we op deze manier 35 dagen opgeschoven, wat het eerste veelvoud van 7 (het aantal dagen in de week) is dat we tegenkomen op deze manier. De juliaanse kalender herhaalt zich dus om de 7*4=28 jaar. Dit maakte het dus heel makkelijk om van een bepaalde datum de dag van de week te berekenen. Er waren namelijk niet zo heel veel mogelijkheden, en terug tellen of vooruit tellen was vrij eenvoudig.

Dit alles veranderde natuurlijk bij de invoering van de ingewikkeldere schrikkeljaar-regels van de gregoriaanse kalender: nog steeds is deze kalender periodiek, maar de periode bedraagt nu maar liefst 400 jaar (303*365 + 97*366 = 146.097 dagen, wat exact 20.871 weken zijn). Ook hier zit er een vast stramien in de 14 mogelijke kalenderjaren, maar aangezien het nu 400 jaar duurt eer dit zich herhaalt, is het een stuk moeilijker om hier gebruik van te maken. Wat is het belang hiervan vraagt men zich af? Inderdaad, in de huidige digitale wereld neemt men gewoon zijn/haar favoriete calendar-app op de smartphone, en zoekt men dit op. Maar enkele tientallen jaren geleden was dit nog niet zo evident, laat staan enkele honderden jaren geleden. En als de katholieke kerk de datum van Pasen wou bepalen, zijnde de eerste zondag na de eerste volle maan van de lente, moet men natuurlijk om te beginnen wel weten wanneer de zondagen in een bepaald jaar juist vallen. Hiertoe voerde men reeds in de tijd van de Romeinen de zogenaamde Littera Dominicalis of zondagsletter in. Deze letter duidt aan op welke dag de eerste zondag van het jaar valt: A voor 1 januari, B voor 2 januari, enzovoort tot en met G voor 7 januari. In een gewoon jaar kan je dus relatief makkelijk per zeven dagen verder tellen om zo alle zondagen uit te rekenen. Aangezien de eerste zondag van 2019 op 6 januari viel, was 2019 een zogenaamd F-jaar.

Bij schrikkeljaren zoals 2020 en 2024 zit je dan echter met een probleem, aangezien er dan op 29 februari ineens een dag extra tussengegooid wordt, waardoor alle dagen van de week vanaf dan een dag opschuiven. De oplossing die men hiervoor bedacht was gebruik maken van een dubbele zondagsletter: de eerste die de zondagen in januari en februari aanduidt, en de tweede die geldt vanaf 1 maart. 2020 is op die manier een ED-jaar. De eerste zondag viel op 5 januari, en dus waren ook 12, 19 en 26 januari zondagen, net als 2, 9, 16 en 23 februari. Moesten we in een gewoon jaar zijn, zou de volgende zondag op 2 maart vallen, net als in een gewoon E-jaar. Maar aangezien er plots sprake is van een extra dag op het einde van februari, zal de eerstvolgende zondag op 1 maart vallen, net zoals in een D-jaar (tel maar na).

Als je dus wil weten op welke dag van de week een bepaalde datum (sinds de invoering van de gregoriaanse kalender) valt, is het dus in principe voldoende om te weten welke zondagsletter(s) bij het jaartal hoort. Aangezien het uiteraard niet in ieders mentale capaciteiten ligt om een 400-jarige cyclus van zondagsletters van buiten te leren, werden hier door wiskundigen tabellen voor opgesteld. Deze konden worden raadgepleegd, bijvoorbeeld op sommige astronomische klokken. Dit soort klokken werd ontwikkeld om bepaalde astronomische gegevens te kunnen aflezen, zoals de stand van maan, zon, sterrenbeelden en planeten, en bevatten vaak ook cyclische kalenderinformatie, zoals bijvoorbeeld de datum van Pasen en aanverwanten. Astronomische klokken komen over heel Europa voor, bijvoorbeeld in Praag, Straatsburg en Kopenhagen, maar ook dichter bij huis in de Zimmertoren in Lier en in het Sint-Agnes begijnhof in Sint-Truiden (deze laatste bevat zelfs het grootste astronomisch compensatieuurwerk ter wereld, gebouwd door Kamiel Festraets). Onderstaande foto's komen uit de Zweedse stad Lund, waar in de plaatselijke kathedraal Lunds Domkyrka een prachtvoorbeeld van zo'n klok, het zogenaamde Horologium mirabile Lundense, te zien is.

Zoals op de linkse foto te zien is, bestaat de klok in Lund uit twee grote delen, in het midden gescheiden door een tafereel van Maria en Jezus (waar tweemaal dagelijks, rond 12u en 15u, de Drie Wijzen en hun knechten passeren, begeleid door het kerstlied In Dulce Jubilo, gespeeld door het kleinste van de vijf orgels van de kathedraal, dat zich in de klok zelf bevindt). Bovenaan is het echte astronomische gedeelte, waar onder andere de maanstanden en de plaats aan de horizon waar de zon ondergaat op af te lezen valt. Het onderste stuk is de ingenieuze kalender dewelke een onuitputtelijke bron van informatie bevat.

Jammer genoeg is er online niet onmiddellijk een rechtstreekse handleiding voor de kalender of de klok te vinden. Maar met een beetje hulp van het wereldwijde web en enkele detailfoto's is het toch mogelijk geweest om te ontcijferen wat er allemaal af te lezen valt op deze kalender. In het midden van de schijf vinden we de jaartallen van 1923 tot 2123 terug (in 1837 werd de klok opgeborgen, en pas in 1923 terug bovengehaald en gerestaureerd, vandaar dat de huidige kalender in 1923 start). Bij elk jaartal horen de volgende gegevens, van buiten naar binnen (klik op de links voor meer informatie): Littera Dominicalis; Numerus Aureus; Cyclus Solis; Cyclus Epactarum; Cyclus Indictionum; Quinquagesima; Dies Paschalis; Pentecoste.

De buitenkant van de schijf bevat informatie per dag van het jaar. Naast de huidige datum, die wordt aangeduid door een metalen pin (mijn bezoek was dus op 13 augustus), vinden we een letter die dient om de dag van de week voor een bepaalde datum te berekenen (hier komen we nog op terug). Daarnaast zien we ook nog de Zweedse naamdagen, het gouden getal (in het rood), de oude Romeinse telling van de dagen in een maand, en de feestdagen van heiligen in de christelijke traditie.

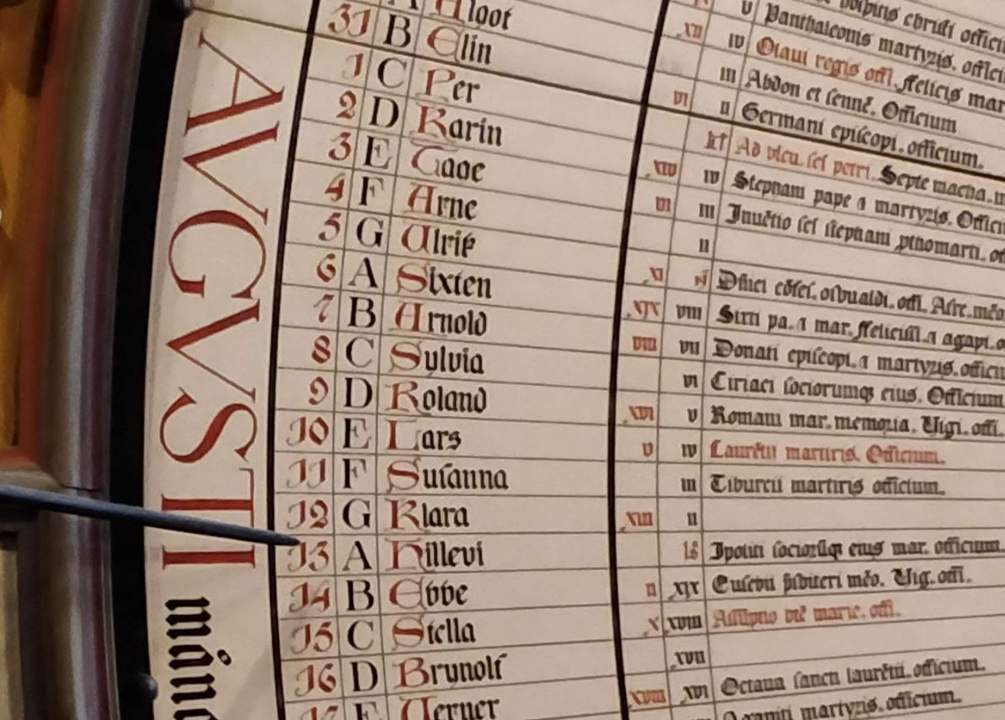
De dagen van het jaar werden gelabeld net zoals bij de zondagsletters: 1 januari is A, 2 januari is B, ..., 7 januari is G, 8 januari is terug A, enzovoort. Met behulp van de letter onmiddellijk naast de datum kunnen we dus heel eenvoudig de weekdag bepalen die bij een bepaalde datum hoort, in combinatie met de zondagsletter van het jaar. We leggen dit uit aan de hand van de dag van mijn bezoek, 13 augustus 2019.

De letter horende bij 13 augustus is de A. We zagen eerder al dat de zondagsletter van 2019 de letter F is, wat maakt dat we weten dat alle F-dagen op een zondag zullen vallen. Van daaruit kunnen we dan ook makkelijk verder tellen, aangezien dan alle G-dagen op maandag zullen vallen, en dus de A-dagen op dinsdag. 13 augustus 2019 was met andere woorden een dinsdag. Je kan dit alles ook samenvatten in een tabel, zodat je de dag van de week maar hebt af te lezen: bovenaan staan de zondagsletters van het jaartal, links de letter van de datum waarvan je de dag wilt weten. Nogmaals met hetzelfde voorbeeld: 2019 is een F-jaar, dus we kijken in de kolom onder F. Vermits 13 augustus een A-dag is, lezen we op de A-lijn af dat dit een dinsdag was.

Ook voor schrikkeljaren kunnen we dit doen, al moeten we dan een beetje opletten. Zoals eerder reeds gezegd, bestaat de zondagsletter van een schrikkeljaar uit 2 letters, eentje die dient om te rekenen voor 29 februari, en eentje om te rekenen erna. 2020 is zoals gezegd, en zoals ook op de klok te zien, een ED-jaar. We bekijken even hoe dit dan in z'n werk gaat:

• 1 januari is per definitie een A-dag. Vermits 1 januari voor 29 februari valt, gebruiken we de eerste van de zondagsletters, zijnde de E. Deze combinatie levert ons in bovenstaande tabel woensdag op, wat wil zeggen dat 1 januari 2020 op een woensdag zal vallen.

• 1 mei daarentegen is een B-dag (tel maar na), en valt na 29 februari. We zoeken dus in de kolom van de tweede letter, zijnde de D, op de B-rij, en vinden dat 1 mei 2020 een vrijdag zal zijn.

• Merk op dat 29 februari zelf geen letter heeft toegekend gekregen, aangezien deze datum niet in elk jaar voorkomt. Je kan uiteraard wel de dag van de week voor 28 februari (C) uitrekenen in een schrikkeljaar met behulp van de eerste zondagsletter van het jaar, en daaruit die van 29 februari afleiden. Of je bepaalt de dag van 1 maart (D) aan de hand van de tweede zondagsletter, en leidt daaruit die van 29 februari af. Beide opties geven, uiteraard, hetzelfde resultaat.

Had je vroeger dan altijd bovenstaand tabelletje en een retour-ticket met paard en koets naar de dichtsbijzijnde astronomische klok nodig om de dag van de week bij een bepaalde datum uit te rekenen? Neen hoor! Knappe koppen, zoals bijvoorbeeld Carl Friedrich Gauss, hebben in de loop van de geschiedenis verschillende algoritmes ontwikkeld om dit te doen. De meeste van deze algoritmes gebruiken ook nog een of andere tabel om getallen in op te zoeken, afhankelijk van het jaar of de datum die je zoekt. Maar er bestaan er ook volledig onafhankelijk van enig opzoekingswerk, die je dus (in principe) volledig uit het hoofd kan doen.

Er bestaan ook nog andere elegante trucs om data uit het hoofd te bepalen. De bekendste is misschien wel de zogenaamde doomsday rule, in 1973 ontwikkeld door de Brit John Conway. Mits wat oefening kunnen deze algoritmes en trucs zeker en vast tot wat leiden. John Conway zelf kan meestal in minder dan 2 seconden het correcte antwoord bij een willekeurige datum geven. Er bestaat zelfs een tweejaarlijks wereldkampioenschap hoofdrekenen, waarbij een van de disciplines is om in een minuut zo veel mogelijk juiste weekdagen bij willekeurige data (1600-2100) te plaatsen. Andere disciplines zijn onder andere het vermenigvuldigen van twee getallen met 8 cijfers of de vierkantswortel berekenen van getallen met 6 cijfers. 

Het wereldrecord kalenderrekenen? Dat staat op naam van de Amerikaan Yusnier Viera Romera, die in januari 2018 maar liefst 140(!) correcte antwoorden gaf, ook hier binnen slechts 1 minuut. Ook al verjaart deze held op 26 april en niet op 29 februari, toch is ook hij een beetje Superman!