Wist je dat ...
-
... het vandaag $\boldsymbol \pi$-dag is? Waarom? Omdat in de Amerikaanse schrijfwijze de datum 14 maart genoteerd wordt als 3/14 en 3,14 is een benadering voor het getal $\pi$.
-
... sinds 26 november 2019 dankzij Unesco:
- ... het getal $\pi$ een constante is die de verhouding geeft van de omtrek van een cirkel tot de diameter? Of de verhouding van de oppervlakte van de cirkel tot het kwadraat van de straal? Merk op dat er helemaal geen regelmaat zit in de decimalen van het getal $\pi$, waardoor het berekenen van veel decimalen van $\pi$ niet evident is. Gelukkig zijn er algoritmes waarmee je $\pi$ relatief snel kan berekenen.
-
... het Europees record memoriseren van decimalen van $\pi$ sinds 7 maart 2020 in handen is van de Zweed Jonas von Essen (29 jaar), met 24063 decimalen? Het wereldrecord staat sinds 2015 op naam van de Indiër Suresh Kumar Sharma (nu 24 jaar), met 70030 decimalen.
-
... het $\pi$-record van november 2016 sinds de vorige $\pi$-dag al twee keer gebroken is? In 2016 berekende Peter Trüb $\pi^e$ biljoen decimalen van $\pi$. Dus 22 459 157 718 361 cijfers. De computer begon de berekening op 29 juli en was ermee klaar op 11 november 2016.
Ter vergelijking: in 1946 berekende ENIAC, de eerste echte elektronische computer, 2037 decimalen van $\pi$ in 70 uur.
Daarbij werd de formule van Machin gebruikt: $$\frac{\pi}{4} = 4 \cdot {\rm Bgtg} \frac{1}{5} - {\rm Bgtg} \frac{1}{239} .$$
-
... op $\pi$-dag 2019 werd bekendgemaakt dat Emma Haruka Iwao, Developer Advocate bij Google, in de cloud 31 415 926 535 897 (dus 31,4 biljoen) decimalen van $\pi$ had berekend. Rekentijd: 121 dagen.
Op 29 januari 2020 werd een punt gezet achter de berekening (en de controle) van de eerste 50 biljoen decimalen van $\pi$ door Timothy Mullican. Het rekenen nam 303 dagen in beslag. Voor beide records werd de volgende formule van de gebroeders Chudnovsky gebruikt:$$ {1\over\pi}=12\sum_{k=0}^{\infty}{(-1)^k(6k)!\over(3k)!(k!)^3} {13591409+545140134k\over 640320^{3k+3/2}} .$$ -
... in het beruchte proces van O.J. Simpson de geloofwaardigheid van de FBI-getuige special agent Roger Martz (een scheikundige van de FBI Forensic Science Research Unit, in Quantico) in twijfel werd getrokken omdat hij niet in staat was om de waarde van het getal $\pi$ te geven?
Cartoon van Tegan Phillips:
- ... indien je op de meest gebruikte rekentoestellen $(1.5)!$ (1,5 faculteit dus, ! staat bij MATH/PRB) intikt, dat je dan een getal krijgt dat met $\pi$ te maken heeft? Welke waarde krijg je dan?
-
... M38 een grote sterrenhoop is in het sterrenbeeld Auriga (Voerman) waar je in de constellatie van de helderste sterren de Griekse letter $\pi$ zal herkennen? En dat Robert Matthews in 1995 de positie van de sterren aan de hemel heeft gebruikt om een benadering van $\pi$ te vinden (titel van de publicatie: Pi in the sky)?
-
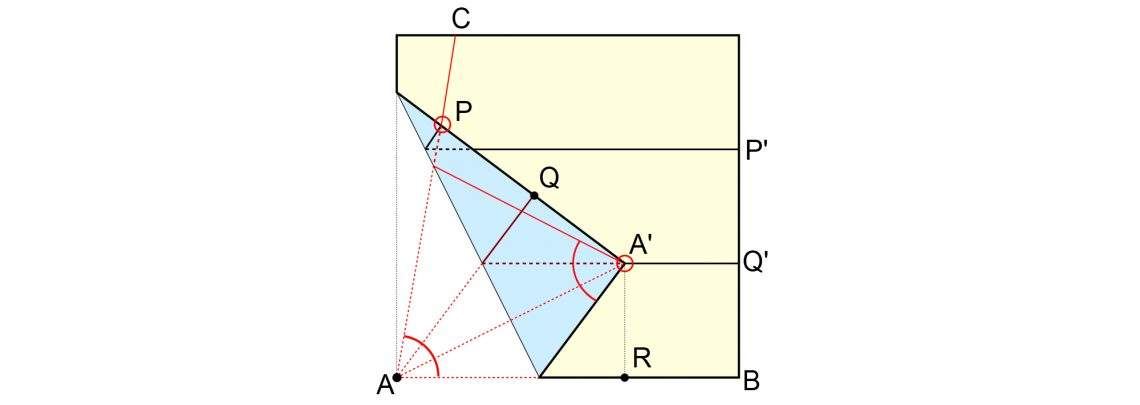
... van de drie Delische problemen uit de oudheid (enkel met passer en liniaal (1) een hoek in drie gelijke delen verdelen, (2) een `kubus verdubbelen' d.w.z. $\sqrt[3]{2}$ construeren en (3) het getal $\pi$ construeren) enkel (3), ook wel de kwadratuur van de cirkel genoemd, niet oplosbaar is met origami? Hieronder zie je een oplossing voor (1).
- ... weerman Armand Pien dit jaar precies 100 jaar geleden geboren werd, en dat hij de BV is die het meeste gedaan heeft voor de bekendheid van het getal Pi? Als we stripfiguren bij BV's mogen rekenen, dan zou het Piet Pienter zijn.
- ... je de eerste 127 decimalen van $\pi$ kan onthouden met behulp van het volgende gedicht (waarvan de auteur onbekend is):
Que j'aime à faire apprendre ce nombre utile aux sages!
Er is ook dit gedicht, van Amanda Gefter:
Immortel Archimède, artiste ingénieur,
Qui de ton jugement peut priser la valeur?
Pour moi, ton problème eut de pareils avantages.
Jadis, mystérieux, un problème bloquait
Tout l'admirable procédé, l'œuvre grandiose
Que Pythagore découvrit aux anciens Grecs.
0 quadrature ! Vieux tourment du philosophe
Insoluble rondeur, trop longtemps vous avez
Défié Pythagore et ses imitateurs.
Comment intégrer l'espace plan circulaire?
Former un triangle auquel il équivaudra?
Nouvelle invention : Archimède inscrira
Dedans un hexagone ; appréciera son aire
Fonction du rayon. Pas trop ne s'y tiendra:
Dédoublera chaque élément antérieur;
Toujours de l'orbe calculée approchera;
Définira limite ; enfin, l'arc, le limiteur
De cet inquiétant cercle, ennemi trop rebelle
Professeur, enseignez son problème avec zèleIt's a clue.
(Een woord met 10 letters staat voor het cijfer 0.)
A never repeating or ending chain, the total timeless catalogue,
elusive sequences, sum of the universe.
This riddle of nature begs:
Can the totality see no pattern, revealing order as reality's disguise? - ... in de 19de eeuw werd bewezen dat de kwadratuur van de cirkel (zie vroeger) onmogelijk is, maar voor die tijd er heel wat grote koppen waren die het toch probeerden?
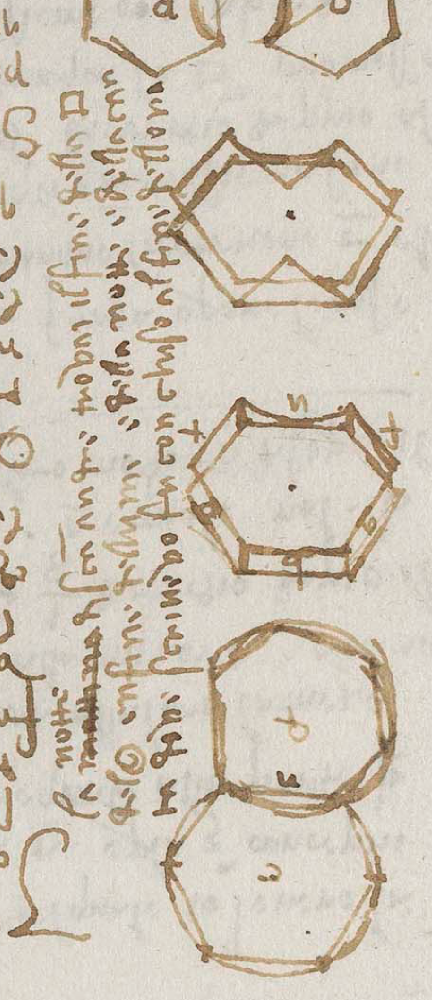
Onder hen Leonardo Da Vinci, die in de kantlijn van een van zijn notaboeken schrijft dat hij klaar is met het probleem: ``In de nacht van Sint-Andreasdag maakte ik een einde aan de kwadratuur van de cirkel." Waarschijnlijk was dit in het jaar 1504. Hieronder zie je een detail (na wat spiegelen;-).
- ... er ook limericks zijn over $\pi$?
There once was a girl who loved pi
I never could quite fathom why
To her it's a wonder
To me just a number
Its beauty revealed by and by(Tom Wilson)
-
Picasso, ondanks zijn naam, geen schilderij heeft gemaakt van het getal $\pi$, maar dat er wel andere kunstenaars geïnspireerd zijn door $\pi$ (bijvoorbeeld Squared Circle (1968), Crockett Johnson)?
