MegaFavoriete Getallen

Of het zinvol is om een favoriet getal te hebben, is nog maar de vraag, maar feit is wel dat vele mensen er een noemen als je hen die vraag stelt, vaak zelfs ogenblikkelijk. Meer dan eens heeft dit getal dan een speciale betekenis in hun persoonlijke leven (de dag van hun verjaardag of huwelijksjubileum, hun huisnummmer, ...) of heeft het een religieuze betekenis of zit er cultureel bijgeloof achter (zie bijvoorbeeld dit overzichtje van enkele getallen en hun symbolische betekenis). Een chemicus antwoordt misschien met het atoomnummer van zijn/haar favoriete element, fans van The Hitchhiker's Guide to the Galaxy antwoorden steevast $42$, en Sheldon Cooper heeft alle redenen van de wereld om $73$ als zijn favoriete getal te kiezen (klik op de getallen voor meer uitleg).

Enkele jaren geleden deed Alex Bellos een online onderzoek naar het favoriete getal van mensen waaruit bleek dat 7 het vaakst voorkwam als lievelingsgetal. Bovendien koos de overgrote meerderheid voor kleine getallen: het kleinste getal dat niet genoemd werd, was 110. Niet dat 110 als groot bestempeld moet worden in de oneindigheid van getallen om uit te selecteren, maar waarom worden grote getallen zelden gekozen? Deze vraag werd onlangs gesteld op YouTube door onder andere James Grime en Matt Parker, waarmee ze tegelijkertijd de oproep lanceerden om je eigen MegaFavNumbers, zijnde je lievelingsgetallen groter dan een miljoen, met de wereld te delen, vergezeld van de reden waarom dat specifieke getal zo bijzonder is. Wij kunnen natuurlijk niet achterblijven.

Stijns megafavoriete getal: 1 591 292

Het getal $\pi$ tart al eeuwenlang de verbeelding van wiskundigen, en de decimalen van $\pi$ bevatten vele eigenaardigheden en mysteries. Het is een nog onbewezen vermoeden dat elk mogelijk getal ergens voorkomt in deze oneindige cijferreeks van decimalen, hoe lang dit getal ook is. Laten we alvast eens kijken naar de eerste 100 cijfers na de komma van $\pi$:

$3.14159\,26535\,\,89793\,23846\,\,26433\,83279\,\,50288\,41971\,\,69399\,37510$
    $58209\,74944\,\,59230\,78164\,\,06286\,20899\,\,86280\,34825\,\,34211\,70679$

Het eerste getal van 1 cijfer dat voorkomt na de komma, is uiteraard het getal $1$ (startend op de 1e plaats na die komma). $1$ blijkt ook het eerste getal van 1 cijfer te zijn dat 2 keer voorkomt: op de 1e plaats en op de 3e plaats. Zoeken we naar het eerste getal van 1 cijfer dat 3 maal voorkomt, dan vinden we op plaatsen 4, 8 en 10 het getal $5$. Het eerste dat 4 maal voorkomt is het getal $3$: op plaatsen 9, 15, 17 en 24. Enzovoort.

Hetzelfde kunnen we doen voor getallen van 2 cijfers. Het eerste getal van 2 cijfers dat 1 keer voorkomt is $14$, maar het is al snel duidelijk dat het eerste getal van eender welke lengte altijd op plaats 1 begint, en dus niet zo interessant is als zoektocht. Boeiender wordt het als we net zoals hiervoor op zoek gaan naar getallen die voor de eerste keer meerdere malen voorkomen. Het eerste 2-cijferige getal dat 2 maal voorkomt is dan ook $\color{red}{26}$, startend op plaats 6 en op plaats 21:

$3.14159\,\color{red}{26}535\,\,89793\,23846\,\,\color{red}{26}433\,83279\,\,50288\,41971\,\,69399\,37510$

Het eerste getal van 2 cijfers dat 3 maal voorkomt is $\color{blue}{93}$, op plaats 14, 42 en 45:

$3.14159\,26535\,\,897\color{blue}{93}\,23846\,\,26433\,83279\,\,50288\,41971\,\,6\color{blue}{93}9\color{blue}{9\,3}7510$

En binnen die 100 decimalen hierboven vinden we ook het eerste getal van 2 cijfers dat 4 maal voorkomt ($\color{red}{62}$, op plaats 20, 72, 75 en 82), maar bijvoorbeeld ook het eerste getal van 3 cijfers dat 2 maal voorkomt ($\color{blue}{592}$, op plaats 4 en 61):

$3.141\color{blue}{59\,2}6535\,\,89793\,2384\color{red}{6\,\,2}6433\,83279\,\,50288\,41971\,\,69399\,37510$
    $58209\,74944\,\,\color{blue}{592}30\,78164\,\,0\color{red}{62}8\color{red}{6\,2}0899\,\,8\color{red}{62}80\,34825\,\,34211\,70679$

We kunnen zo in het algemeen op zoek gaan naar het eerste getal van $k$ cijfers dat $n$ maal voorkomt in de decimalen van $\pi$, al heb je er dan uiteraard al snel veel meer dan 100 nodig. We krijgen dan onderstaande tabel, met het aantal cijfers $k$ in de bovenste rij en het $n$-maal voorkomen in de linkerkolom:

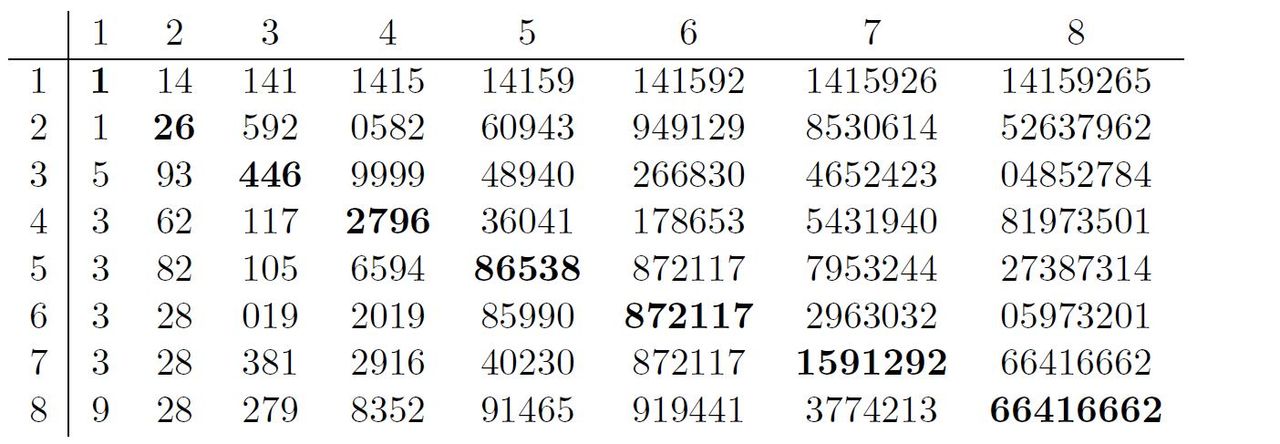
Merk op dat getallen in deze context met een 0 kunnen starten. Zo is $019$ het eerste getal van 3 cijfers dat 6 maal voorkomt, en $0582$ het eerste getal van 4 cijfers dat 2 maal voorkomt. Bijzonder zijn de getallen op de diagonaal van de tabel (in het vet), zijnde de eerste getallen van $n$ cijfers die $n$ keer voorkomen (rij A331881 in de Online Encyclopedia of Integer Sequences):

$1, 26, 446, 2796, 86538, 872117, 1591292, 66416662, \ldots$

Aangezien de opdracht was om een favoriet getal groter dan een miljoen te kiezen, kiest Stijn voor het eerste getal van 7 cijfers dat 7 maal voorkomt in de decimalen van $\pi$: $1\,591\,292$.

Pauls megafavoriete getal: $2^{257}-1$

Ofwel voluit geschreven:

$231\,584\,178\,474\,632\,390\,847\,141\,970\,017\,375\,815\,706\,539\,969\,331\,281\,128\,078\,915\,168\,015\,826\,259\,279\,871$

Iets minder bescheiden in grootte-orde, maar daarom niet minder interessant wat het verhaal erachter betreft.

Naast de decimalen van $\pi$ en alles wat daar mee te maken heeft, is er nog een constante in de geschiedenis van wiskundigen over de hele wereld en hun fascinaties: de priemgetallen. We keren terug naar het begin van de 17e eeuw en reizen naar het koninklijk paleis in Parijs (toen kon dat nog zonder verplichte quarantaine), waar we in een monnikscel een zekere Marin Mersenne terugvinden: zowel priester als wiskundige van opleiding. De Mersennepriemgetallen zijn naar hem genoemd: priemgetallen van de vorm $2^p-1$ waarbij $p$ zelf een priemgetal is. Maar let op, niet elk priemgetal $p$ zal op deze manier leiden tot een Mersennepriemgetal. Zo geldt er bijvoorbeeld dat $2^{11}-1 = 2047 = 23 \times 89$. In 1644 publiceerde hij een lijst van elf priemgetallen van dit type, waarvan hier de eerste acht:

Mersenne stelde dan wel deze lijst op, maar het was de Zwitserse wiskundige Leonhard Euler die honderd jaar later pas bewees dat $M_{31}$ effectief een priemgetal was. (Voor de liefhebber: Euler bewees eerst dat alle mogelijke priemfactoren van $M_{31}$ rest 1 of rest 63 moeten hebben bij deling van $M_{31}$ door 248, en dan controleerde hij handmatig alle priemgetallen van die vorm die kleiner zijn dan $\sqrt{M_{31}}$. Euler was op dat ogenblik volledig blind, wat zijn prestatie nog indrukwekkender maakt.) De drie andere getallen op de lijst van Mersenne waren $M_{67}$, $M_{127}$ en $M_{257}$. Maar helaas, hier liep het tweemaal mis.

Een van de meest memorabele lezingen uit de geschiedenis van de wiskunde werd in 1903 gegeven door Frank Cole, toenmalig secretaris van de American Mathematical Society. Gewapend met een stukje krijt in de hand, begon hij vol goede moed aan de (handmatige) berekening van $2^{67}$ op het bord. Van het resultaat trok hij 1 af, en schreef de einduitkomst onderaan op het bord: $147\,573\,952\,589\,676\,412\,927$. De rest veegde hij af, en begon al even handmatig het product $193\,707\,721 \times 761\,838\,257\,287$ te berekenen. U raadt het al: een tijdje later bleek de uitkomst van dit product perfect overeen te komen met de eerder berekende $2^{67}-1$. Een lezing waarbij Cole geen woord had gezegd, maar de aanwezigen beloonden hem terecht met een staande ovatie: Frank Cole had namelijk bewezen dat Mersenne ongelijk had, en dat $M_{67}$ geen priemgetal was.

Cole gaf later toe dat hij drie jaar lang iedere zondag had gezocht naar de ontbinding van $M_{67}$ als product van twee getallen. Maar die overgave verdwijnt in het niets bij de toewijding van Édouard Lucas: Lucas offerde 19 jaar lang zijn vrije tijd op om uiteindelijk in 1876 te bewijzen dat $M_{127} = 170\,141\,183\,460\,469\,231\,731\,687\,303\,715\,884\,105\,727$ wel degelijk een priemgetal is. Hier had Mersenne in zijn oorspronkelijke lijst dus wel gelijk. Het is nog altijd het grootste priemgetal ooit dat op handmatige wijze verkregen is, en pas 75 jaar later zou er (met behulp van computers) een groter priemgetal gevonden worden. Tussendoor zouden er nog drie Mersennepriemgetallen ontdekt worden die niet in de oorspronkelijke lijst stonden: $M_{61}$ (Pervushin, 1883), $M_{89}$ (Powers, 1911) en $M_{107}$ (Powers, 1914).

Voortbouwend op het werk van Lucas, was het Derrick Henry "Dick" Lehmer die een test ontwikkelde om na te gaan of getallen al dan niet priem waren: de zogenaamde Lucas-Lehmertest. Voor grote getallen moest er nog steeds veel gerekend worden, maar voor Mersennegetallen viel dit al bij al nog wel mee. De Belgische wiskundige Maurice Kraitchik gebruikte die test in 1922 om te bewijzen dat het laatste getal van Mersenne's oorspronklijke lijst, $M_{257}$, geen priemgetal was. Hij was echter niet honderd procent zeker van zijn berekeningen -- terecht, want Kraitchik rekende er nogal eens naast -- en dus riep hij de hulp in van Lehmer. Die kon in 1927 het resultaat bevestigen door gebruik te maken van een mechanische machine met negentien fietskettingen, een machine die hij samen met zijn vrouw Emma Lehmer, beter bekend als Emma Lemma, had gebouwd.

De fietskettingen-machine die Lehmer bouwde was trouwens de voorloper van zijn foto-elektrische zeef die hij in 1932 ontwikkelde en waarmee het slechts enkele minuten duurde om tien miljoen kandidaat-delers voor een bepaald getal te controleren. Hiermee slaagde hij er in om bijvoorbeeld $M_{93} = 2^{93}-1$ te factoriseren, iets waar een ijverige mens die tien uur per dag rekent zo'n honderdduizend jaar voor nodig zou hebben (beweerde Lehmer zelf). Het was de voorloper van computers die sinds de jaren 50 gebruikt worden voor priemtesten en voor het vinden van nieuwe, steeds maar grotere (Mersenne)priemgetallen. In 1952 deed SWAC (de Standards Western Automatic Computer) er bijvoorbeeld maar 48 seconden over om te bewijzen waar Lehmer en zijn vrouw 700 uur aan besteedden: $M_{257}$ is geen priemgetal.

Long story short: het duurde dus bijna 300 jaar om de oorspronkelijke lijst van Mersenne te controleren. De lijst bleek vijf fouten te bevatten: drie Mersennepriemgetallen werden over het hoofd gezien, en twee getallen stonden ten onrechte op de lijst. Het grootste getal dat op de lijst stond, $M_{257}$, bleek jammer genoeg een van die indringers te zijn die niet op hun plaats waren, wat door een Belgische wiskundige in 1922 met de hand werd geverifieerd en later door een machine gebouwd met fietskettingen werd bevestigd. En daarom is dit getal het megafavoriete getal van Paul.

#MegaFavNumbers

Tot slot delen we graag enkele van onze favoriete online inzendingen (in opklimmende volgorde van grootte van het getal in kwestie, zonder kwalitatieve rangschikking van onzentwege), allen zeker het bekijken waard:

• Michael Erskine over het getal $79\,873\,884$

• James Grime over het getal $666\,030\,256$ (en $696\,630\,544$)

• Ben Sparks over het getal $906\,150\,257$

• Zoe Griffiths over het getal $61\,218\,182\,743\,304\,701\,891\,431\,482\,520$

• NormalizedNerd over het getal $115\,132\,219\,018\,763\,992\,565\,095\,597\,973\,971\,522\,401$

• Matt Parker over het getal $1\,169\,809\,367\,327\,212\,570\,704\,813\,632\,106\,852\,886\,389\,036\,911$

• Will Wei over het getal $8\,424\,432\,925\,592\,889\,329\,288\,197\,322\,308\,900\,672\,459\,420\,460\,792\,433$

• 3Blue1Brown over het getal $808\,017\,424\,794\,512\,875\,886\,459\,904\,961\,710\,757\,005\,754\,368\,000\,000\,000$

• Katie Steckles over het getal Megiston