Harvey Friedman maakt er zijn levenswerk van om onbereikbare wiskunde tastbaar te maken. Later dit jaar neemt de gerenommeerde wetenschapper een positie in als gastprofessor aan de Universiteit Gent. Een gesprek met een man die even hartelijk is als intelligent.
Harvey Friedman is een genie: op zijn achttiende behaalde hij zijn doctoraat in de wiskunde aan het prestigieuze Massachusetts Institute of Technology. Onmiddellijk daarna werd hij benoemd aan de al even respectabele Stanford University. Sindsdien staat hij in het Guinness Book of World Records genoteerd als de jongste professor ooit.
De toenmalig assistent-professor in de filosofie werd later ook professor in de wiskunde en in de muziek, tot hij in 2012 op emeritaat ging. Een jaar daarna ontving hij een eredoctoraat aan de Universiteit Gent. Dit jaar besluit hij de banden met de UGent verder aan te halen: hij wordt er niet alleen gastprofessor in de onderzoeksgroep wiskundige logica van Andreas Weiermann, hij zal er ook een permanent archief inrichten waar zijn werk te consulteren zal zijn.
Tijd voor een gesprek. Maar hoe hou je als interviewer stand tegen iemand die ooit een tekst schreef getiteld ‘Een goddelijk bewijs voor de consistentie van de wiskunde’? Friedman toonde erin aan dat de gebruikelijke wiskunde zonder interne tegenspraak is wanneer men het bestaan van God aanvaardt. Bovendien bleek uit Friedmans deelnames aan voordrachten dat hij bijzonder snel nadenkt en zijn gefundeerde vragen onmiddellijk stelt.
Daarom liet ik me voor dit gesprek ruggensteunen door Weiermann zelf, die mee vragen voorlegde aan Friedman. Het leverde een reeks ongedwongen antwoorden op.
Kunt u uw onderzoek in enkele zinnen aanschouwelijk maken?
‘In de wiskunde stel je vragen waarop je eenduidige antwoorden wil krijgen. Je wil weten of je beweringen waar zijn of niet. Maar in de jaren 1930 ontdekte de Oostenrijkse Amerikaan Kurt Gödel (1906-1978, red.) dat er wiskundige beweringen zijn die je kunt bewijzen noch ontkrachten. Ze zijn totaal onbereikbaar. Gödels werk was nogal abstract en ver verwijderd van de wiskundige realiteit. Het verlangen groeide om zijn werk wat meer down to earth te maken en in verband te brengen met de fysische werkelijkheid.’
‘Daarop heb ik 54 jaar gezocht. Ik stelde tastbare problemen voor die verband houden met Gödels meer filosofische beweringen. Ik formuleerde alledaagse wiskundige vraagstukken die niet kunnen worden beantwoord in de wiskunde zelf (zie kaderstuk 'Alledaags en onopgelost', red.).’
Maakt dat u niet depressief? De Russische wiskundige Vladimir Arnold stelde ooit dat Gödels ontdekking hem enige tijd moedeloos had gemaakt.
‘Maar er is evengoed een positieve kant aan! Wanneer je je methodes uitbreidt op manieren die de wiskundigen nog niet algemeen aanvaard hebben, dan kun je tóch die Gödelse vraagstukken behandelen en er een antwoord op geven. Dat we op die manier die hogere wiskundige principes hebben ontdekt, dat maakt mij juist gelukkig.’
De paradox van de duizendpoot stelt dat het insect nadenkt over hoe het erin slaagt om te lopen en net daarom struikelt. Veel wiskundigen trekken zich wellicht weinig aan van zulke paradoxen volgens Gödel en gaan gewoon door met hun werk ...
‘Ik moet je even onderbreken. Het gaat hier niet om paradoxen, maar om onbewijsbaarheden. Ik beschouw Gödels werk niet als paradoxaal in de aard van de Kretenzer die zei dat alle Kretenzers altijd liegen. Of zoals de paradox van Russell over de verzameling van alle verzamelingen die niet zichzelf bevatten. Gödel gebruikte de ideeën achter die paradoxen wel om zijn resultaten te bekomen. Toch is er een duidelijk onderscheid tussen die paradoxen – die dus tegenstrijdigheden zijn – en Gödels ideeën over bepaalde stellingen. Die laatste zijn onbewijsbaar.’
Dat geldt ook voor een idee van Georg Cantor, de Duitse grondlegger van de moderne verzamelingenleer. Hij bewees dat het aantal elementen van de verzameling van alle deelverzamelingen van een verzameling groter is dan het aantal elementen van de gegeven verzameling.
‘Het aantal elementen van alle deelverzamelingen van alles is ook een ‘aantal’. Maar is dat dan groter dan het ‘aantal’ van alles? Als je erover nadenkt val je snel in een tegenstrijdigheid.’
Die theorie van Gödel is ongeveer een eeuw oud. Toch stoppen vele boeken over de geschiedenis van de wiskunde precies daar. Wat kwam er volgens u daarna?
‘Ik zou zeggen: mijn werk. Maar dat klinkt onbescheiden, nietwaar. Het gaat er eigenlijk om, zoals ik al zei, dat het ten tijde van Gödel niet duidelijk was wat de impact van zijn ontdekking was. Vandaag weten we beter hoe ver zijn ontdekking reikt. Ze zweeft niet ergens in de hogere wiskunde, maar heeft gevolgen tot op het niveau van wiskunde die een aandachtige scholier in de derde graad secundair onderwijs kan vatten. Of zelfs tot op het niveau van het lager secundair.’
In Vlaanderen werd in 1997 de verzamelingenleer in het onderwijs afgeschaft. Het beleid kwam daar 22 jaar later schoorvoetend op terug. Wat vindt u daarvan?
‘Voor begaafde scholieren kan die leer zeer interessant zijn, maar ze is niet noodzakelijk basiskennis. Voor de onderlegde leerlingen valt trouwens zeker nog wat meer te doen. Ik ben in de Verenigde Staten verbonden met het Arnold Ross’s Program, dat zomercursussen wiskunde organiseert. De deelnemers krijgen zelfs oefeningen gebaseerd op een deel van mijn recent werk en kunnen ermee overweg. Het is dus absoluut mogelijk om jongeren er daadwerkelijk mee in contact te brengen.’
'Door onze methodes uit te breiden hebben we hogere wiskundige principes ontdekt. Dat maakt me gelukkig'
‘Overigens vind ik ook dat een cursus wiskundige logica onontbeerlijk is. Het is onbegrijpelijk dat zelfs sommige universiteiten zoiets niet opnemen in het basisprogramma voor bachelorstudenten.’
Hoe schat u het wiskundeniveau in deze regio in?
‘Jullie hebben topwiskundigen genoeg, die belangrijk werk hebben verricht. (Lacht:) Het is niet voor niets dat ik heb besloten de onderzoeksgroep in Gent te vervoegen.’
U zou weleens het pad van Jean Paul Van Bendegem kunnen kruisen, een nogal bekende filosoof verbonden aan de Vrije Universiteit Brussel.
‘Is hij een aanhanger van de ultra-eindigheidstheorie, en erkent hij dus geen oneindige verzamelingen (het bestaan daarvan ontkennen is een andere manier om paradoxen en onbewijsbaarheden te ontlopen, red.)? Of is hij een intuï-tionist, die dus bewijzen uit het ongerijmde weigert (een bewijsmethode die stelt dat het tegenovergestelde van iets niet waar kan zijn, waardoor het gestelde dus wel waar moet zijn, red.)? Hoe dan ook staan mij interessante discussies te wachten.’
Wat beschouwt u zelf als uw mooiste onderzoeksresultaat?
‘Er zijn veel mooie resultaten en bewijzen! Als ik er een zou moeten kiezen, dan wel het bewijs dat de disjunctie-eigenschap de numerical existence-eigenschap impliceert. Dat bewijs verscheen in het tijdschrift Proceedings of the National Academy of Sciences, op voordracht van Kurt Gödel zelf, drie jaar voor zijn dood.’
Welk van uw resultaten had de grootste impact?
‘Mijn werk in omgekeerde wiskunde had nogal wat gevolgen. In dit deelgebied van de wiskundige logica proberen wetenschappers na te gaan welke axioma’s nodig zijn om bepaalde stellingen te kunnen bewijzen. We gaan dus omgekeerd te werk en kijken welke stellingen we wensen te kunnen vooropstellen, en wat daarvoor het minimale aantal grondregels is.’
‘Maar ik hou ook wel van de theorie over binaire bomen en grafen waarnaar je zelf, Andreas, ook veel onderzoek verricht met de mensen van je groep (een binaire boom is een eenvoudig diagram, zoals van een stamboom of een reeks ja-neekeuzes, maar waarin al gauw wiskundige moeilijkheden optreden, red.).’
U bent al lang een liefhebber van schaken. Kunt u een probleem voorleggen?
‘Ik zou er tientallen kunnen geven! Ik werk zelfs aan een wiskundige schaaktheorie en een boek met schaakproblemen van wiskundige aard, maar eigenlijk wil ik ze nu nog niet delen. Sorry about that.’
U heeft ook een passie voor pianomuziek, met name voor die van Vladimir Horowitz, een begenadigd Oekraïens-Amerikaans klaviervirtuoos die bekendstond om zijn contrastrijk spel.
‘Ik denk dat Horowitz piano speelde op het meest creatieve niveau, en dat die creativiteit de essentie is van zijn spel. Ik weet dat ik een nogal ongebruikelijke benadering heb van de wiskunde en van pianomuziek, en ik neem me voor om me daar de komende jaren in te verdiepen. Je kunt je afvragen of er een verband bestaat tussen beide. Natuurlijk is dat er! En ik hoop in de toekomst aan te tonen dat dít verband wél bewijsbaar is.’
Alledaags en onopgelost
Beschouw ‘eindige bomen’, dat zijn eindige verzamelingen van met lijnen verbonden knopen, waarbij voor een gegeven knoop precies één weg bestaat om van deze knoop naar de onderste knoop te gaan. Er zijn dus geen takken die omhoog groeien en opnieuw in elkaar samenvloeien. Een boom heet ‘inbedbaar’ in een tweede boom als er een voorschrift bestaat dat de knopen van de eerste boom naar knopen van de tweede boom afbeeldt en dat de boomstructuur van de eerste boom bewaart. Een rij van bomen, B1, B2, ..., BM heet ‘niet-K-chaotisch’ als voor een gegeven getal K het aantal knopen van de i-de boom hoogstens K+i is. Bijvoorbeeld, als men K=3 neemt, dan mag het aantal knopen van de eerste boom hoogstens 4 zijn, van de tweede boom hoogstens 5, van de derde hoogstens 6, enzovoort. Een (in de rekenkunde) onaantoonbare uitspraak van Friedman luidt nu: voor een gegeven getal K, bestaat er een getal M groot genoeg zodat een willekeurige niet-K-chaotische rij bomen B1, B2, ..., BM, steeds toelaat om twee getallen m en n kleiner dan of gelijk aan M te nemen waarbij m kleiner is dan n én de m-de boom kan worden ingebed in de n-de boom.
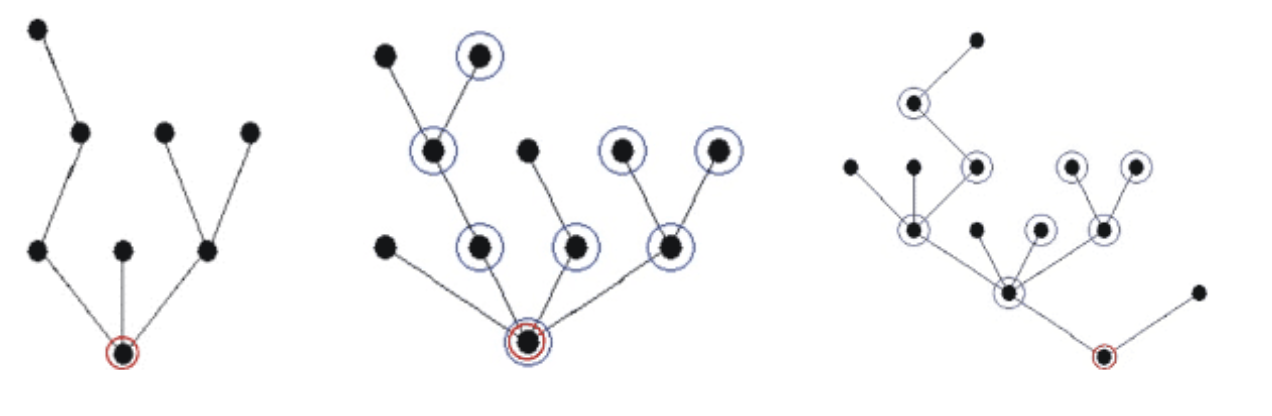
De boom links kan ‘ingebed’ worden in de middelste en in de rechtse boom, zoals aangegeven door de blauwe cirkels. De rode cirkels duiden de wortels aan van de bomen.

In dit voorbeeld is voor K=3 het aantal knopen van de i-de boom niet groter dan 3+1 en de rij bomen is dus niet 3-chaotisch. Maar voor M=10 bestaan er geen getallen m en n kleiner dan of gelijk aan M met m<n waarbij Bm inbedbaar is in een Bn.
Harvey Friedman (°1948) is een Amerikaans wiskundige verbonden aan de Ohio State University in de VS. Hij is gespecialiseerd in de wiskundige logica. In 1974 was hij spreker op het vierjaarlijkse International Congress of Mathematicians, het belangrijkste wiskundecongres ter wereld. Tien jaar later won hij de prestigieuze Alan T. Waterman Award. In 2007 volgde de Tarski Lectures-prijs. Over zijn werk verscheen in 1985 het boek Harvey Friedman’s Research on the Foundations of Mathematics.