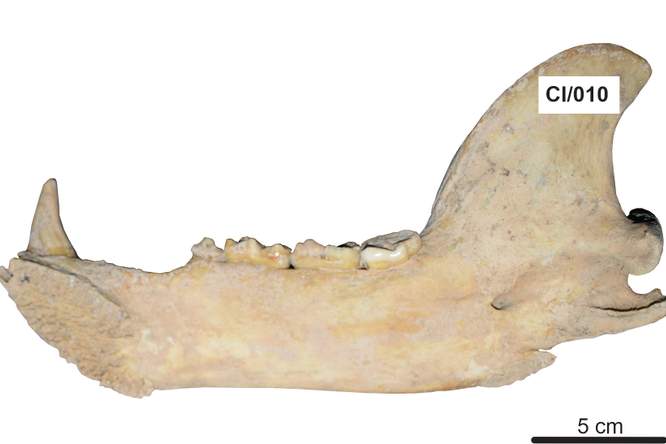
Staat de wieg van de wiskunde in Centraal-Afrika? Een 22.000 jaar oud botje met inkervingen, opgegraven in het Congolese Ishango, doet vermoeden van wel. De ontdekker, Jean de Heinzelin, had op zijn sterfbed nog een verrassing: een tweede Ishangobeentje. Het bleef een halve eeuw in zijn lade liggen. Het kleinood is cruciaal om de verschillende hypothesen over het eerste telstaafje te bevestigen of te ontkrachten.
Dit artikel komt uit ons archief en is terug actueel vanwege het verzoek van het Nationaal Instituut voor Natuurbehoud (ICCN) van Congo aan België om de Ishango-botjes terug te geven.
Eén enkel beentje zou het wel eens kunnen begeven onder het zware gewicht van de hypothesen die er op gestapeld worden’, werd een staande uitdrukking in discussies over het Congolese Ishangobeentje, de oudste onbetwistbare getuigenis van logica en van het begin van tellen. Een tweede Ishangobeentje moet het pleit beslechten.
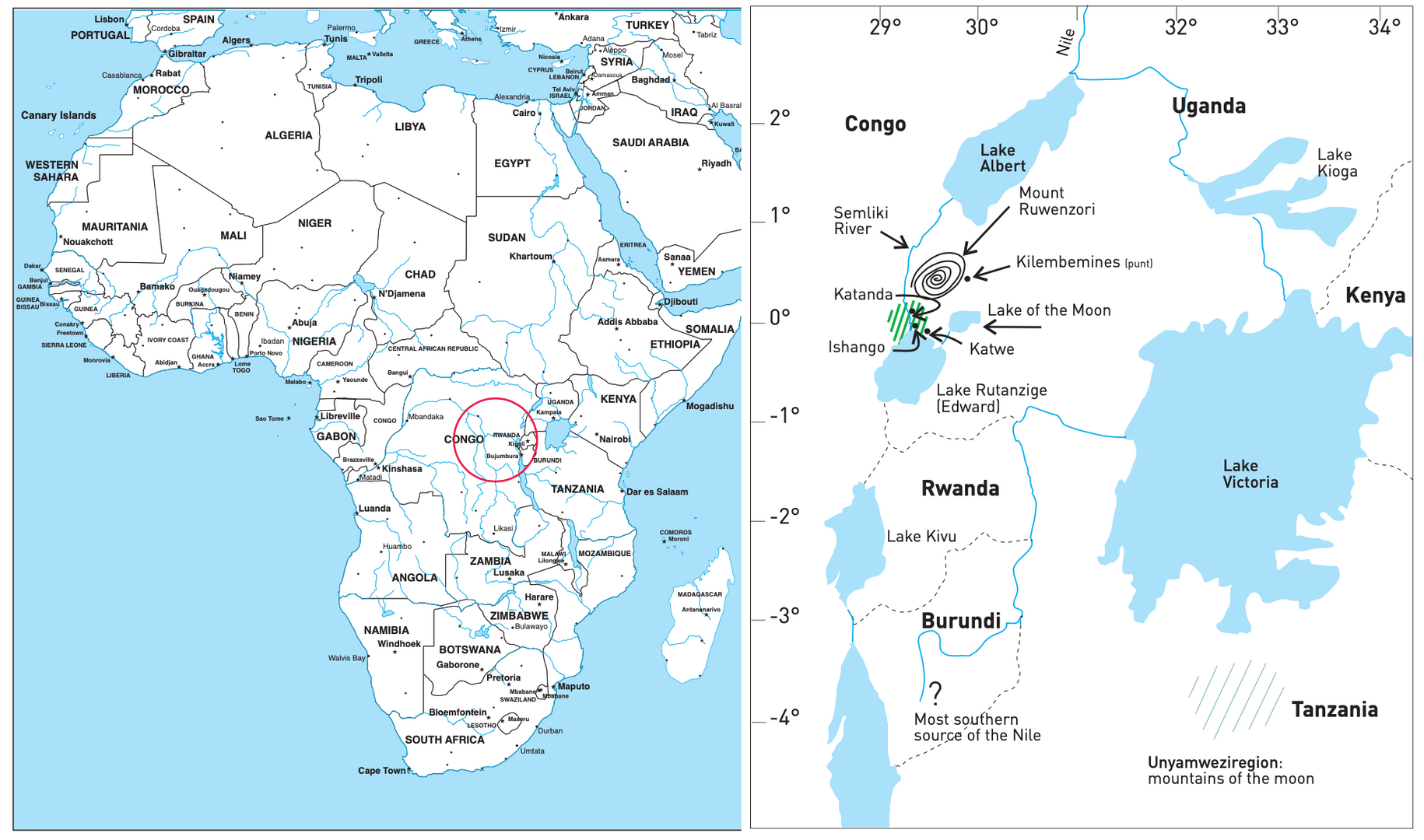
De Brits-Indiase wiskundige George Gheverghese Joseph gebruikte voor het eerst het beeld van de zware hypothesen in zijn nu gerenommeerde oeuvre The Crest of the Peacock (1991), over de geschiedenis van de niet-Europese wiskunde. Toen hij het gedeelte over Afrika voorstelde, merkte Joseph op dat de gegevens niet erg overvloedig waren, in tegenstelling tot, bijvoorbeeld, Arabische, Indische of Chinese wiskunde. Het Ishangobeentje met zijn geordende kerven was een veeleer alleenstaand voorbeeld. Belgisch geoloog-archeoloog Jean de Heinzelin de Braucourt vond het botje op de grens tussen Congo en Uganda, aan de oevers van het Rutanzigemeer (voorheen het Edwardmeer) en de Semlikirivier. Toen schenen gezwollen conclusies over de Afrikaanse oorsprong van de wiskunde vergezocht, en zoals het kritische tijdschrift The Skeptical Inquirer bewees, overheerste een politieke Afro-Amerikaanse agenda soms op de wetenschappelijke.
Maar, ondertussen vulde recent wetenschappelijk onderzoek de gegevens grondig aan. Het staafje bleek 22.000 jaar oud, en niet 8.500 of 11.000 jaar zoals eerder verondersteld. En niet onbelangrijk: in de schatkamers van sommige musea bleken gelijksoortige telstokken te liggen.
De klap op de vuurpijl was een tweede Ishangobeentje, dat voor ongeveer vijftig jaar in een lade had gelegen. De verschillende hypothesen over de betekenis van de eerste Ishangostaaf konden dus worden bevestigd of ontkracht. Eigenaardig genoeg was het pas op het einde van zijn leven, in 1998, dat De Heinzelin zijn notities verzamelde en een kladversie voor een publicatie maakte. Nu, op de vijftigste verjaardag van het eerste verslag over de opgravingen in Ishango, op 28 februari 2007, nemen het Koninklijk Belgisch Instituut voor Natuurwetenschappen (KBIN) van Brussel en het Koninklijk Museum voor Midden-Afrika (KMMA) in Tervuren de uitdaging aan, en maken ze postuum het tweede Ishangobeen openbaar.

Eerste Ishangobeen
De Heinzelin zelf had het Ishangobeentje onder de aandacht van het grote publiek gebracht met een publicatie in Scientific American (1962) en Claudia Zaslavsky (1917-2006) maakte het voorwerp bekend bij het publiek van wiskundigen, de Afro-Amerikanen en Afrikanen in haar boek Africa Counts (1973). Hun verslagen werden sindsdien veelvuldig herhaald.
Het eerste Ishangobeentje is op zich een merkwaardig voorwerp: een klein gebruiksvoorwerp van slechts tien centimeter, met een kwartskristal dat goed vastgezet is aan één uiteinde. Het ziet eruit alsof het een soort schrijf- of graveerwerktuig was, of zelfs een prehistorisch potlood. Hoe dan ook, de meest intrigerende kenmerken blijven de drie kolommen met kerven of sporen die langs de lengteas verspreid staan. Eén ligt aan de gekromde kant en werd door De Heinzelin de M-kolom genoemd (Milieu), de andere zijn aangeduid met G (Gauche) en D (Droite). In elke kolom zijn de ongeveer evenwijdige kerven ingedeeld in duidelijk zichtbare groepen, al verschillen ze van lengte en hebben ze lichtjes andere oriëntaties:
Kolom G: 11 13 17 19
Kolom M: 3 6 4 8
10 (=9+1) 5 5 7
Kolom D: 11 21 19 9
De merktekens van het been intrigeerden De Heinzelin. Hij nam onder meer contact op met Lancelot Hogben, een gewaardeerd wiskundige in De Heinzelins tijd. Hij had toen net het boek Mathematics for the Million geschreven. We citeren even: ‘Basis 2 verschijnt op het been door het principe van de verdubbeling [M-kolom] en de tafel van 4; de basis 10 door haar centrale positie en de herhaling van de bewerkingen die naar 10 verwijzen en de veelvouden ervan, de scheiding van de M<_10, G en D<_9, en de getallen 10±1 en 20±1 [D-kolom]. Daarenboven laat de keuze van de priemgetallen [G-kolom] veronderstellen dat de kennis van de hogere bewerkingen zoals vermenigvuldiging en deling bekend waren. Kortom, het zou een ‘magische tabel’ geweest zijn die een gevorderde rekenkundige kennis toonde: (a) optelling, aftrekking, verdubbeling en vermenigvuldiging (met uitzondering van de deling), (b) basis 2 en 10, waarbij 10 gezien wordt in de vorm ‘9+1’, (c) priemgetallen, (d) het grootste vermelde getal is 21, (e) het grootste getal verkregen door bewerkingen is 60.’
De Heinzelins vriend prof. Libois onderschreef de interpretatie van het rekenkundige spel: ‘De vroegste mens nam de eigenschappen waar van getallen terwijl hij kleine hoopjes keien, beentjes, bonen, graankorrels of pitten manipuleerde’. Omstandig bewijs van etnowiskundige verslagen zou later deze intuïtieve veronderstellingen bevestigen, evenals de veronderstelde vermenging van het gebruik van verschillende bases. Bovendien werden verdubbelingen en halveringen over heel Afrika waargenomen in de zogenoemde vermenigvuldigingsmethode ‘van het platteland’, of nog, in de ‘kleermakersmethode’ van Senegal. De Heinzelins recentere hypothese die stelde dat 3, 5, 7, 11, 13, 17, 19 een lijst van priemgetallen voorstelt (hoewel de orde op de staaf verschillend is), is meer twijfelachtig, net zoals een andere meer recente stelling dat de staaf ook kennis van ‘nul’ weergeeft. Nergens in Afrika ten zuiden van de Sahara werd het gebruik van priemgetallen of nul vastgesteld.
Dit gebrek aan substantieel bewijs contrasteert met de interpretatie voorgesteld door Alexander Marshack. De G- en D-kolom geven een totaal van 60 = 5x12, en de M-kolom 48 = 4x12, wat overeenkomt met twee maan-maanden en een anderhalve maan-maand. Marshack onderzocht het beentje met een microscoop en hield niet alleen rekening met het aantal kerven, maar ook met hun verschil in grootte en vorm, evenals met de volgorde van de deelgroepen. De kleinere en dikkere lijnen zouden de verschillende fasen van de maan aanduiden, in een soort ritme of patroon. Marshack was zijn loopbaan begonnen als gedreven journalist en werd later archeoloog. Hij begon en besloot zijn volumineus werk Roots of Civilization met de veronderstelling dat het Ishangobeen een maankalender was.
Toch is Marshacks interpretatie moeilijk te vatten. Zijn gelijkaardige studie van de benen plaat van Blanchard, uit het Franse Dordogne, werd niet unaniem aanvaard. Bovendien is de staaf duidelijk te klein om daadwerkelijk als een kalender te kunnen worden gebruikt. Wel is het zo dat Afrikaanse beschavingen kalenders maakten met beentjes en touwtjes. De rol van de maan in vele gebruiken werd in de literatuur toegelicht. Sommigen zien zelfs een verband met verzen van Homeros’ Ilias, wanneer de Griekse schrijver stelt dat ‘oi Pygmaioi’ nabij de oevers van de Nijl leefden en ‘verschenen bij de seizoensgebonden verschijning van de kraanvogels, in bloedige gevechten om de oogsten te verdedigen waar ze van leefden’. In Ishango kent het plaatselijke microklimaat echter nauwelijks seizoenen, en leefden de mensen in een welvarende gemeenschap, zonder risico op geregeld terugkerende beproevingen.
Datering
Eén ramp veranderde de Ishangogemeenschap nochtans diep: een grote uitbarsting in het vulkanische gebied van Katwe, enkele kilometer naar het oosten. Ze verspreidde een meters dikke laag van as en tuf over een aanzienlijk gebied.
De vulkaanuitbarsting hield een voordeel in voor de reconstructie van de geschiedenis van de Ishangosite: het is een goedbewaarde opeenvolging van op elkaar gestapelde lagen, van lithisch en beenderig materiaal. Er waren geen sporen van structuren voor bewoning, want de lagen bestonden alleen uit opeenvolgende toevoegingen van ‘afval’ van woonsten aan de oever, zoals een nijverheid met kleine kwartskristallen, maalstenen, grijprollers, pijlen, haken, en een grote hoeveelheid van gepolijste beenderen. De Heinzelin kon nauwkeurig het ontstaan onderscheiden van verschillende types van visharpoenen. Het toont dat Ishango een bevoorrechte plaats was voor een beschaving, en permanent bewoond was.
Nadeel van de vulkanische uitbarsting van Katwe was dat ze het water van het meer met tellurisch CO2 overlaadde, en dit voor een lange tijd. Deze inerte overvloed aan C12 verouderde en veranderde de gebruikelijke verhoudingen van isotopen in het water van het meer zo erg dat zelfs moderne schelpen gedateerd werden op 1.000 vóór Christus (zelfs lang na de uitbarsting van Katwe). Ook in de atmosfeer was de verhouding C14/C12 niet noodzakelijk constant en niet gelijk aan de huidige zodat de koolstofhoeveelheid niet als een referentie kan worden gebruikt. Daarom hield De Heinzelin, een geoloog, het bij een ‘algemene stratigrafische chronologie’, gebaseerd op de aanwijzingen van hoogte, omgeving, grondontleding en gevonden afzettingen. Het leidde hem tot een benadering van 8.000 vóór Christus, dat wil zeggen de overgangsperiode van pleistoceen tot holoceen; deze datering zou hij steeds blijven verdedigen.
Het meningsverschil met de rest van de archeologische onderzoeksgemeenschap kan een van de redenen geweest zijn waarom De Heinzelin niet erg aangemoedigd was om zijn Ishangorapporten voort te zetten, en voorrang te geven aan zijn andere meer universeel aanvaarde vondsten. Verdedigers van een ‘absolute tijdsbepaling’ dateerden de schelpen van Ishango door het radiocarbon. Zij dateren de Ishangostaven nu tussen 21.000 en 23.000 vóór Christus. De Heinzelin was gevoelig voor hun argumenten en hij wees zelfs op hun werk: ‘We kunnen niet voorbijgaan aan de opgravingen van John Yellen, die plaatsvonden in 1988-1989 in Katanda, drie kilometer stroomafwaarts op de rechteroever van de Semliki. Een nijverheid gekenmerkt door dikkere harpoenen dan die van Ishango werd geassocieerd met paleolithische kenmerken. Ze is duidelijk ouder […]’. Inderdaad, een ouderdom van 90.000 jaar bleek correct voor deze andere sites gelijksoortig aan Ishango. In deze context lijkt de stelling dat de cultuur die de Ishangostaven maakte, ongeveer 22.000 jaar oud was, nog vrij voorzichtig.
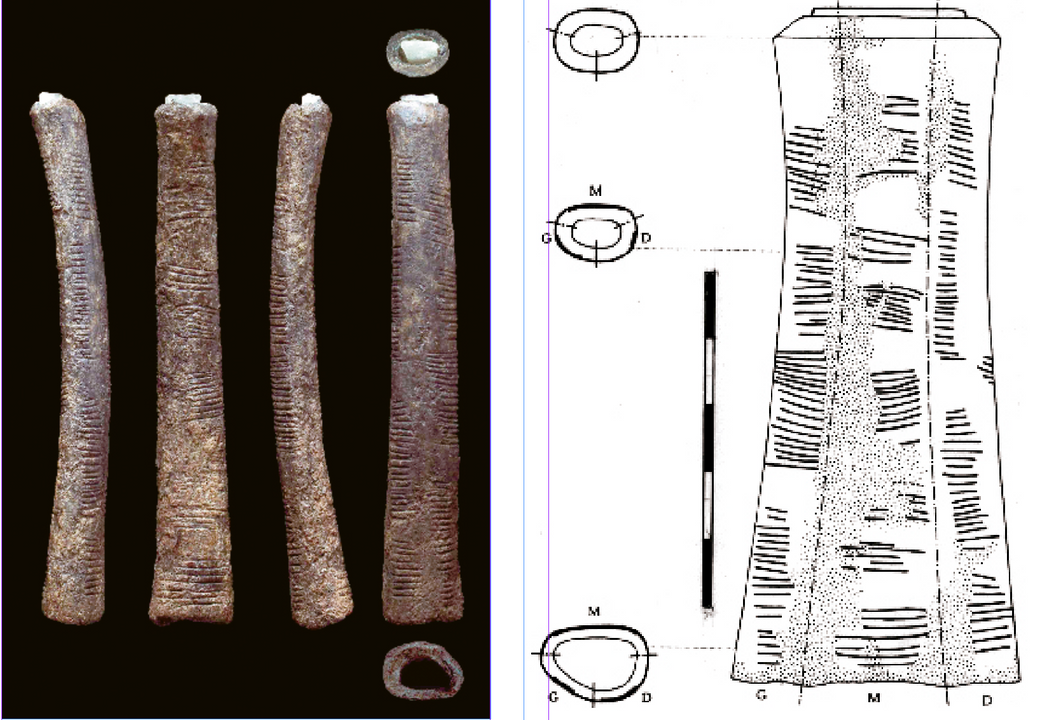
Links: het eerste Ishangobeen vanuit zes verschillende perspectieven. Rechts: De Heinzelins tekening, uit 1957, waarop de groeven duidelijk te zien zijn.
Geïsoleerd
De toekenning van de ontdekking van rekenkundige begrippen aan een kleine groep van neolithische mensen in het hart van Afrika is volgens een meer algemene kritiek erg verrassend. De gemeenschap zou afgesneden geleefd hebben van andere belangrijke nederzettingen. Nochtans lijkt deze relatieve isolatie niet te beantwoorden aan wat historici over gebieden in de omgeving te weten zijn gekomen. Ten zuiden en ten oosten van de Sahara bestonden paden voor culturele of commerciële uitwisselingen, en ook de route van Ishango over Khartoem naar Egypte langs de Nijl, en van Khartoem naar West-Afrika werd door bepaalde historici aanvaard, al rees geleidelijk twijfel over de betekenis van die route. De contacten tussen bevolkingsgroepen impliceerden niet noodzakelijk een culturele uitwisseling, en de duidelijke verbanden tussen de vroege Ishangocultuur en de bosjesmannen wierp een ander licht op de geografische richting van eventuele uitwisselingen.
Zelfs een van de meest aantrekkelijke kenmerken van Ishango, namelijk zijn ligging aan de huidige bronnen van de Nijl (samen met het Victoriameer en het kleinere Meer van de Maan), verloor haar betekenis. Het ‘terras’ waar de opgravingen gebeurden, ligt ongeveer tien meter hoog boven de huidige bedding van de Semlikirivier, maar enkele duizenden jaren geleden voerde de rivier ijsstromen af van de Ruwenzori. De archeologische site van Ishango is dus een rivierdelta van een ijsmeertje op de flanken van het Ruwenzorigebergte. De vorming van de delta duurde lang en toont dat er permanent kustbewoning was van vissers, jagers en plukkers. Slechts in recente tijden hebben geografische veranderingen het water van de Semliki naar de Nijl doen vloeien.
Ondanks dit alles mag men niet uitsluiten dat er in oude tijden een geprivilegieerde route langs de Nijl bestond voor de export van exotische producten vanaf de grote meren van Centraal-Afrika naar de oevers van de Middellandse Zee. Toch werd de verspreiding van de Ishangobeschaving naar het Noorden, net voor het faraotijdperk van Egypte, al aangetoond door de vergelijking van korte harpoenen, gevonden in Khartoem en in het gebied van Turkana.
Andere inkervingen
Ten tijde van Josephs boek, The Crest of The Peacock, en de daaropvolgende kritiek over het belang van Ishango, was het inderdaad waar dat de meeste artefacten zoals het Ishangobeen gevonden waren in Europa, van het Iberische schiereiland tot de Russische steppen. Marshacks Roots of Civilization bevatte voor het grootste deel acheologische vondsten uit Europa, maar dat komt doordat in Afrika toen gewoon minder opgravingen werden uitgevoerd. Vandaag evenmin. Geïnspireerd door de tijdsbepalingen van 75.000 tot 90.000 jaar voor de vrij moderne, getande harpoenen gevonden bij de Semlikirivier, staat in de huidige tekstboeken dat de moderne mensen vernuftige gebruiksvoorwerpen hadden vooraleer ze zich vanuit Afrika naar andere continenten verspreidden. In Europa werden zulke voorwerpen voor het eerst uitgevonden 40.000 jaar geleden.
De wiskundige verzuchtingen van de vroege mens kunnen ook bepaald worden in het licht van hun waarschijnlijkheid, vermits de gegroepeerde logische kerven op de Ishangostaven lijken voorafgegaan door eenvoudiger telopnamesystemen of gekerfde tekeningen. In de grotten van de Lebombobergen in Zuid-Afrika bijvoorbeeld werd in 1987 een fossiel been van een aap gevonden, dat 35.000 jaar oud is en 29 kerven vertoont. Een andere steen van ongeveer 70.000 jaar oud, beschreven in 2001, heeft bijna evenwijdige lijnen en bewijst de vaardigheid van de vroege mens om bijna meetkundige tekeningen te maken. De Ishangostaven bleven gelukkig bewaard, terwijl andere, houten stokken en teltouwtjes de tijd niet doorstonden. Tot in de 20ste eeuw bleven voorwerpen om hoeveelheden op te noteren wijdverspreid. De ontdekkers en missionarissen hechtten zelden belang aan die oninteressante kerfstokken of geknoopte touwen. Toch werden ze soms opgemerkt, zoals in de expeditie van Grant en Speke, waar de dragers touwtjes gebruikten. Uitzonderlijk schonken missionarissen of koloniale beheerders toch enkele telvoorwerpen aan een museum. Het Koninklijk Museum voor Midden-Afrika in Tervuren neemt hierin een speciale positie in, omdat de katholieke clerus – wegens hun bijzondere aandacht voor opvoeding – zelfs verslagen over het gebruik van de gekerfde stokken of geknoopte touwtjes bijvoegden. Ze kunnen in de bibliotheek van het KMMA nog altijd worden geraadpleegd. Over het algemeen vertellen deze beschrijvingen verhalen over het tellen van dagen, weken, maanden of jaren, en waarom sommige speciale gebeurtenissen moesten worden onthouden (zoals de troonsbestijging van een nieuwe koning). Andere delen het vastleggen mee van betalingen, leningen, verdeling van water, te vervoeren goederen, verkochte ivoren tanden enzovoort.
Sture Lagercrantz besteedde drie lange overzichtsartikelen aan Afrikaanse telkoorden, telstokken, en sneden in of tatoeages op het lichaam. ‘Tellen door middel van stenen, nootjes, stokken, grasblaadjes en gelijkaardige voorwerpen is een oud gebruik dat in het bijzonder werd opgemerkt in Zuid-Sudan. De telmethode kan vergeleken worden met die van teltouwtjes. Die laatste waren meer verspreid naar het noorden, maar ze behoorden tot dezelfde zwarte cultuur. De oude culturele elementen behelzen ook het tellen met lijnen getekend op de grond, op deuren en muren.’
Zaslavsky beschreef hoe de Fulani van Niger in Noord-Nigeria twee korte stokken in de grond staken in de vorm van een V, om aan te duiden dat ze 100 dieren hadden, terwijl een kruis, een X, 50 aanduidde. Horizontale stokken duidden 10 aan, verticale de eenheden, en dus betekende = ||| 23, terwijl VVVVVVX|| stond voor 652. In recente tijden, werden deze beweringen uitgebreid gestaafd. Dr. Mubumbila Mfika, een scheikundige uit Gabon, reproduceerde de diagrammen van de Bashongo uit Oost-Congo, die lijnen in het zand trokken met drie vingers van één hand, en drie groepjes van drie met één lijn aanvulden: ||| ||| ||| |. De Bambala telden per vijf, maar de Bangongo, Bohindu en Sungu per vier. De telgebaren en hun creatieve noteringssystemen leggen gedeeltelijk de verschillen uit in de gebruikte bases in Afrika. Recente verslagen tonen dat de bases 10 of 12 zeker niet de enigen waren: linguïsten ontdekken tot op vandaag het gebruik van bases zoals 2, 5, 6, 12, 16, 20, of zelfs 32. Zo zeggen sommige volkeren niet 17 als ‘7 en 10’, maar als ‘3 van de 20’ of als ‘5 en 12’, of gebruiken voor 37 uitdrukkingen zoals ‘3 minder dan 2-20’ of ‘32 plus 5’. De telgewoontes spreken tot de verbeelding en gaan terug naar de oudste tijden, zoals Lagercrantz uitwees (met een onvrijwillige allusie naar Ishango): ‘De oude gewoontes om het aantal gedode vijanden te tellen door kerven op de eigen huid van de krijger, was erg verspreid in het gebied rond het Albertmeer (het Rutanzigemeer), en aan de andere kant in het centraal gebied van Zuid-Afrika. Dit bevestigt goedgedocumenteerde etnografische verbanden tussen Noordoost-Afrika en zuidelijk Afrika.’

Honderdjarige gekerfde stokjes uit de schatkamers van het KMMA in Tervuren (catalogus: EO.0.0.1816; EO.0.0.34992; EO.0.0.2144; alle foto's: ADIA, KBIN Brussel; alle voorwerpen: verzameling KMMA (c)).
Tweede been broodnodig
Recente vondsten suggereren een derde interpretatie van de Ishangostaaf. De Heinzelins ‘rekenkundige spel’ met priemgetallen, zonder vermelding van andere rekenkundige feiten zoals kwadraten of derde machten zou een eigenaardige overgang geven van elementair tellen naar een abstract begrip. Marshacks interpretatie als maankalender wordt niet bevestigd in de traditionele Afrikaanse kalenders op geknoopte touwtjes en stokken, die simpelweg dagen opsomden, zij het over een langere periode. Toch vraagt de onmiskenbare logica op het been om een uitleg, maar die hoeven we misschien niet verder te zoeken dan dat het een gewone getuigenis is van een telmethode die de bases 6 en 10 vermengde. Zo’n telproces komt zelfs gangbaar over naar westerse maatstaven: bijvoorbeeld, wanneer het resultaat van een verkiezing moet worden geteld op een papier of een bord, worden getallen dikwijls gegroepeerd per 5, en vervolgens in twee groepjes van vijf, omdat de basis 10 gebruikelijk is in het Westen: |||| ||||; |||| ||||; |||| |||| … Hoeveelheden van kleine voorwerpen, zoals centjes of fiches, worden daarentegen dikwijls geteld in paren: 2, 4, 6, 8, 10, … Bovendien worden op een lat dikwijls streepjes van verschillende lengte aangebracht: ||||||||||||||| …
Als de Ishangogemeenschap bijvoorbeeld haar woord voor 7 als ’één-drie-drie’ had uitgesproken, dan zou het waarschijnlijk zijn dat de kerven dit ‘vertalen’ als ||||||| , en dit was het geval op de staaf. De kerven voor 10, in de middelste M-rij, tonen 9+1, en dit brengt onwillekeurig het hedendaagse woord in het Swahili voor de geest voor het getal negen, namelijk ‘kenda’, wat zoveel betekent als ‘neem één weg’. De enige duidelijke rekenkundige bewerking op de Ishangostaaf, de verdubbeling, kan op dezelfde manier geïnterpreteerd worden, vermits 8 in vele Afrikaanse talen of in tekeningen in het zand als ‘ne-na-ne’, wordt begrepen, en dit is ‘vier-en-vier’. Natuurlijk kon dit dan weer op zijn beurt geleid hebben naar de vermenigvuldigingsmethode zoals die in Egypte, West-Afrika of Ethiopië werd vastgesteld.
Als niet de vermenging van een basis 10 en 2 maar van een basis 6 en 10 de gewoonte was geweest in Ishango, dan zou dit uitleggen waarom de sommen van de kolommen 60 en 48 zijn. Analoog zouden immers bij een vermenging van de bases 10 en 2, meer groepen van 100, of 20 en 40, zijn opgedoken. Dus zou het wel eens kunnen, naar analogie van de D-kolom die een duidelijk patroon van 10±1 en 20±1 toont, dat de G-kolom zich laat lezen als 12±1 en 18±1, eventueel voorafgegaan door het einde van de M-kolom, waar 5 en 7 kunnen staan voor 6±1.
Bewijs voor deze vermenging van bases bestaat overvloedig. De Nyali-telwoorden combineren 4 en 6, terwijl N. Thomas in 1920 de bases 6 waarnam bij woorden van 7 tot 9 in Guinee. De Bulanda drukten 10 uit als 6+4 de Bola 12 als 6x2 en 24 als 6x4. Het is merkwaardig vast te stellen dat Thomas’ artikel dateert van 1920, lang voor de ontdekking van de Ishangostaven. Hij suggereert een ‘vanzelfsprekend’ verband tussen de duodecimale getalwoorden in sommige gebieden van Nigeria en de Semlikiregio. In zijn tijd kon hij er natuurlijk alleen aan denken dat de rekenkundige concepten vanuit Egypte langs de Nijl werden uitgevoerd naar deze gebieden in zwart Afrika.
Pletser, een fysicus en een ingenieur, deed een extra stoutmoedige suggestie dat er een verband zou bestaan tussen de verschillende kolommen, zoals de mogelijkheid dat de 13 op de G-kolom de som zou zijn van de 3-6-4 in de middelste kolom. Dit doet denken aan de oude rekenliniaal die ingenieurs gebruikten toen er nog geen rekenmachine was, maar het zou ook een eenvoudig gevolg kunnen zijn van de ordening van de rijen kerven in kolommen. Wanneer, bijvoorbeeld op een bord, twee rijen van kerven |||| |||| … worden neergeschreven, die ene onder de andere, dan worden ze dikwijls gerangschikt zodat het eerste teken van elke rij precies onder de ander wordt geschikt, volgens eenzelfde onzichtbare verticale lijn. Die relatie tussen een grafische voorstelling en de overeenkomstige teltechniek kan dan op zijn beurt weer indirect gevolgen gehad hebben voor het rekenen, zoals Pletser aanwees. Al bij al maakt deze meer afgewogen interpretatie het Ishangobeen minder spectaculair, omdat het geen priemgetallen noch sterrenkunde impliceert, en geen beroep doet op een wiskundige ‘overkill’. Misschien was dat maar goed ook, maar de ultieme test zou nog volgen.
De opgravingen in Ishango vonden plaats tussen 1950 en 1959 in verschillende fasen. In de laatste bracht Marcel Spinglaer, de hoofdtechnicus die in het departement van De Heinzelin werkte, een ander gekerfd been mee. Het legt uit waarom het gedetailleerde rapport van 1957 het bestaan ervan niet vermeldde en waarom de publicatie in 1962 in Scientific American, die een samenvatting was, erover zweeg. Het duurde jaren om de informatie over het tweede been ter beschikking te krijgen, en de bevestiging van Pletsers interpretatie moest al die tijd wachten, wat de spanning natuurlijk opdreef.
Het tweede been werd gevonden in een niveau dichtbij het eerste, zonder enig verschil voor wat de tijdsbepaling betreft. Ter herinnering, de uitgegraven lagen waren gevormd door huishoudelijk afval, en niet door funderingen van woningen, zodat het onzeker blijft of beide ‘beenkervers’ elkaar kenden of niet. Het is echter wel erg waarschijnlijk dat ze in een gelijksoortige omgeving leefden en een gelijksoortige opvoeding genoten.
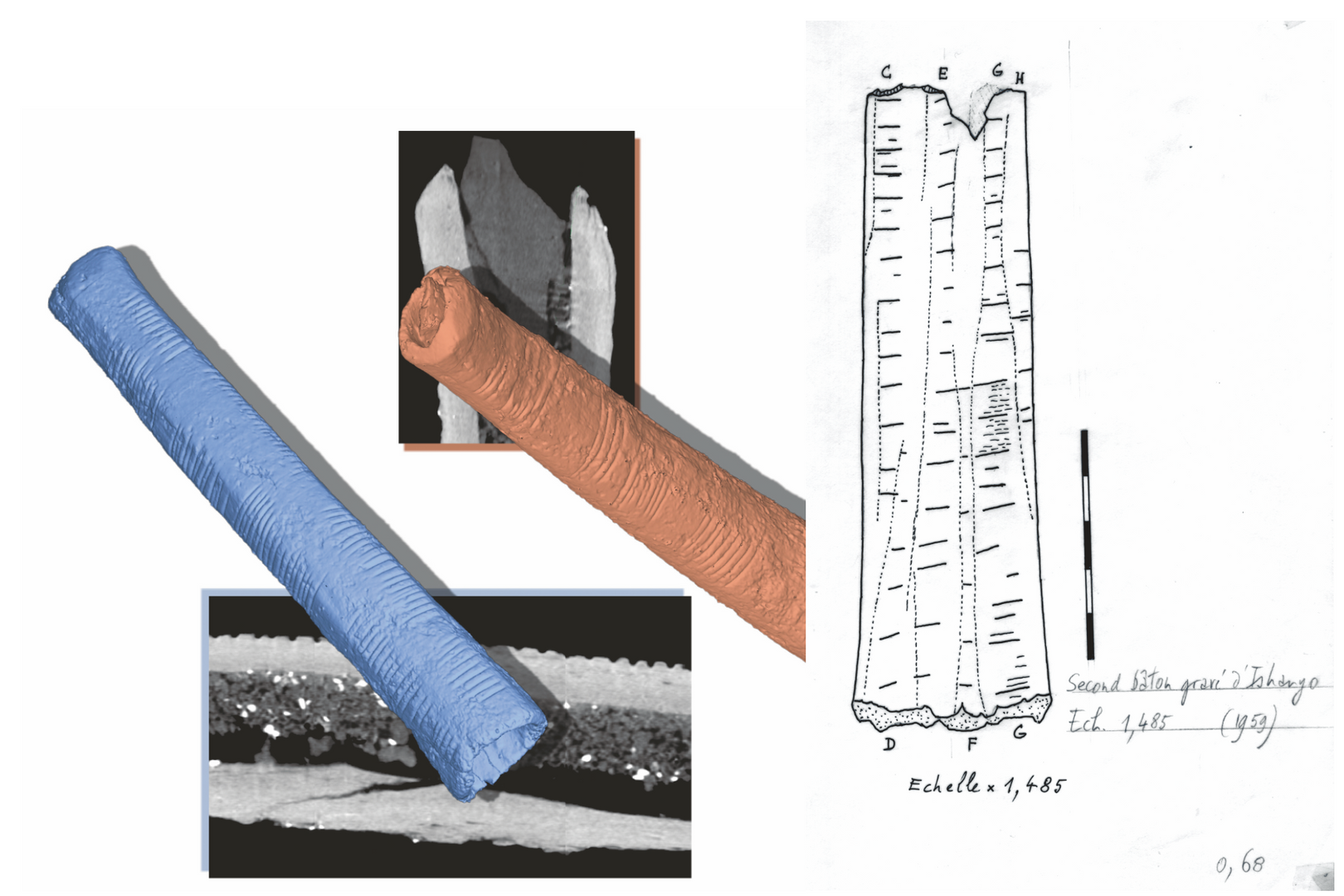
Links een 3D-beeld van het eerste beentje, gemaakt met een medische scanner. Daarop is het binnenste te zien en de manier waarop de kristal is vastgezet. Rechts een tekening van het tweede Ishangobeentje, een toetssteen voor vele hypothesen over het eerste wiskundige kerfstokje.
Het been is een beetje langer, en heeft een holle sectie in het midden, een schacht van een lang been waarvan de anatomische bepaling tot op de dag van vandaag twijfelachtig is. Het been schijnt recht te zijn gemaakt door schrapen en gladschuren en is goed bewaard, zij het gebroken op één uiteinde. Wellicht was er een kwartskristal in bevestigd, zoals het geval was voor het eerste beentje, wat dus bevestigt dat de Ishangocultuur voorwerpen gebruikte voor kerven, schrijven of zelfs met didactische doelstellingen.
Het tweede been heeft 6 rijen, die De Heinzelin nummerde met C, D, E, F, G en H:
C: 14 lange kerven; 6 korte.
D: 6 lange kerven.
E: 17 lange kerven; 1 korte.
F: 6 lange.
G: 20 lange.
H: 6 lange kerven; 2 korte.
De Heinzelin voegde eraan toe dat de kleine kerf op de E-kolom op de ‘plaats van 10’ staat en verwonderde er zich over of dit ‘een overgang van de basis 10 naar 12 betekende’. Hier volgt een meer gedetailleerde beschrijving van de meer problematische G-kolom:
Korte 4’; korte 6’; twee korte tweelingkerven tussen 7 en 8; een korte kerf 9’ na 9; mat gedeelte tussen 10 en 12 (twee getalbases?); twee korte kerven 18’ en 18’’ tussen 18 en 19 (of derden?); vier korte kerven tussen 19 en 20 (of vijfden?); korte 20’.
Omdat de C-rij een totaal van 20 kerven heeft, en de E-rij 18 (de korte kerven zijn hier tamelijk lang), lijken de bases 6 en 10-20 te zijn gebruikt. Meer nog, er zijn twee ruimtelijke overeenkomsten tussen de rijen, bij E10 = F1 = G10 en bij E12 = F2 = G12.
Toetssteen
Het is duidelijk dat er nu geen priemgetallen zijn, noch dat een kalender van maan-maanden onderscheiden kan worden. In de dagen voor zijn dood, scheen De Heinzelin zelf Pletsers hypotheses van een vermenging van bases 6 en 10 en de rekenlat te hebben aangenomen, hoewel hij Pletser nooit gekend heeft: ‘Dit doet ons enigszins denken aan de equivalentie tussen de twee basissen 10 en 12 (decimaal en duodecimaal). Men moet de herhaling van de 6 eenheden van de korte rijen in verband brengen met de matte delen van G tussen 10 en 12. De nadruk met de kleine kerven verantwoordt het idee van een rekenlat.’
De kwartskristallen op de Ishangobeentjes maken de vondst intrigerender dan de telstokken uit de schatkamers van de hedendaagse Afrikamusea en van de beschrijvingen door missionarissen en beheerders. Omdat het Ishangovolk haar getallen bedacht in een basis 6-10 combinatie, zoals volkeren in zovele Afrikaanse gebieden vandaag, komt een onmiskenbare logica te voorschijn, al dan niet met opzet. Dit werd in 1999 door de auteur van dit artikel voorgesteld, gebaseerd op etnowiskundige vergelijkingen op het eerste staafje, zonder het tweede te kennen. Natuurlijk moet het belang van de ontdekking nog worden aangetoond: heeft de vermenging van de Ishangobases 6-10 inderdaad Egypte bereikt? Ofwel, werd het Ishangovolk naar het zuiden geduwd, naar het huidige Botswana? We kunnen alleen hopen dat archeologen meer opgravingen in Afrika zullen doen, of dat etnologen ook eens naar hun collecties zullen kijken door een wiskundige bril, in het belang van de exacte wetenschappen, en vooral in het belang van Afrika zelf.
Dankwoord
Dirk Huylebrouck, Departement Architectuur Sint-Lucas (Brussel) dankt Ivan Jadin en Patrick Semal, Koninklijk Belgisch Instituut voor Natuurwetenschappen (Brussel) en Els Cornelissen, Koninklijk Museum voor Midden-Afrika (Tervuren), alsook Vladimir Pletser van het European Space Research and Technology Centre (ESTEC, ESA) (Noordwijk). De hulp van het KMMA en van de ADIA-groep van het KBIN bij het vinden van de passende illustraties werd ook erg op prijs gesteld.