Weersvoorspellingen gebeuren vandaag de dag aan de hand van stevige computermodellen op supercomputers. Met enkele eenvoudige wiskunde technieken geraak je echter ook al ver.
Als je tegenwoordig naar het weerbericht kijkt, zit daar stevige rekenkracht achter. We zijn in staat om het weer van de komende dagen nauwkeurig te voorspellen dankzij modellen die fysische vergelijkingen vertalen in code. Om die code op fijne schaal te kunnen doorrekenen, draaien supercomputers dag en nacht en verwerken ze continu nieuwe informatie. Maar moet het altijd zo ingewikkeld zijn? Hoewel minder nauwkeurig, geraken we al ver met relatief eenvoudige wiskunde.
Zal het vandaag regenen?
Stel je voor: je zit ’s ochtends aan het ontbijt, en je twijfelt of je met de fiets of de auto naar het werk zal gaan. Gisteren ben je namelijk door de regen overvallen tijdens het fietsen, en dat wil je niet nogmaals voorhebben. Als je nu die informatie gebruikt om de kans te bepalen dat je vandaag natgeregend zal worden, ben je al wiskundig bezig. Proficiat!
De overgang tussen natte en droge dagen (of van nat naar nat en droog naar droog) kan namelijk vrij eenvoudig weergegeven worden. We kunnen voor elk van deze overgangen de kans bepalen. Stel bijvoorbeeld dat als de vorige dag nat is, de kans dat het de volgende dag nat is 70% bedraagt. De kans dat het de volgende dag droog is, bedraagt dan 30%. Als je deze informatie zou gebruiken om te beslissen of je al dan niet zou fietsen, maak je gebruik van een Markovketen. Dit is een systeem waarbij de overgang tussen verschillende toestanden als een kans beschreven wordt en we altijd tussen deze toestanden blijven variëren. De hier voorgestelde nat-droogketen zou je kunnen weergeven zoals in de figuur hieronder. Het lijkt misschien eenvoudig, maar dit principe wordt regelmatig gebruikt als basis om neerslag te modeleren.
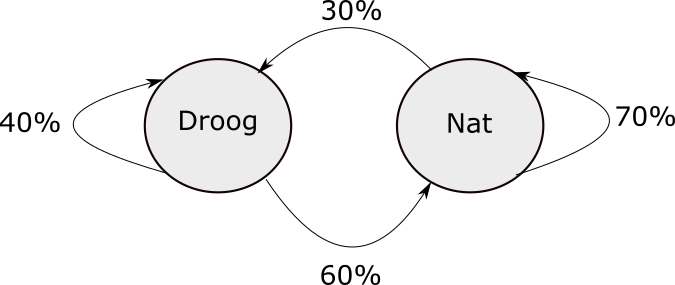
Hoe warm was het vanmiddag?
Je hebt uiteindelijk toch gefietst en had geluk: het regende niet. Je kreeg het wel al best warm tijdens het fietsen, dus wanneer je ’s avonds thuiskomt, werp je snel een blik op de thermometer aan de fietsenstalling. Die geeft weer dat het ondertussen nog maar 10° C is. Ben je iets met die informatie?
Wat je kan doen, is rekening houden met de verandering van de temperatuur doorheen de dag. Vanaf zonsopgang stijgt de temperatuur, tot ze rond de middag een hoogtepunt bereikt. Doorheen de namiddag begint zakt de temperatuur langzaam, tot ze ’s nachts kort voor zonsopgang het laagst is. Vervolgens begint de opwarming weer. Op die manier ontstaat een golfpatroon, en dat kunnen we gebruiken om de temperatuur in te schatten. Als je ongeveer weet hoe de golf zich gedraagt en op welk punt van de golf je temperatuursmeting zit, kan je het hoogtepunt bepalen. Zo’n golven worden meestal weergegeven door middel van een sinusfunctie. Dat beestje doet je misschien terugdenken aan hoekberekeningen, maar heeft daarnaast nog veel meer toepassingen.
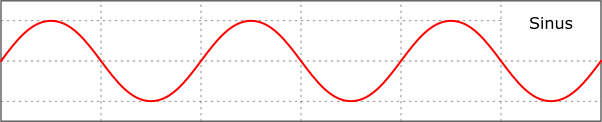
Een typisch voorbeeld is het reconstrueren van uurlijkse temperatuursmetingen aan de hand van het dagelijkse maximum. Verschillende meetstations houden namelijk enkel de maximale dagtemperatuur bij, hoewel uurlijkse data vaak veel praktischer zijn om fysische fenomenen beter te begrijpen of een impact in te schatten. Door een aantal keer uurlijks te meten, kunnen we de sinusfunctie opstellen en die vervolgens blijven gebruiken.
Wat zegt de temperatuur over regen?
We zijn ondertussen een week later. Ondanks dat je rekening hield met het weer van de voorgaande dagen, ben je toch tweemaal nat op het werk aangekomen. Toegegeven: dat is het nadeel van kansrekenen. Je beslist dus om het over een andere boeg te gooien: je vraagt je thuiswerkende partner om ’s middags de temperatuur te bekijken. Kan je met die maximale dagtemperatuur aan de slag gaan om de neerslag ’s avonds te bepalen? Dan ben je in ieder geval zeker dat je niet nat thuiskomt.
Een van de mogelijkheden die je hebt, is om een ruwe relatie op te stellen tussen temperatuur en neerslag: we kunnen ervan uit gaan dat wanneer het warmer wordt, er minder regen zal zijn. Het kan natuurlijk dat dat verband niet helemaal op gaat: af en toe kan het warmer zijn en valt er regen, of hebben we een koude dag met een stralende zon. De maat die aangeeft hoe sterk ons verband is, is de correlatie. In het geval van het voorbeeld hier gegeven, zal deze richting -1 moeten gaan. Dat betekent dat als de temperatuur stijgt, de hoeveelheid neerslag vermindert, en omgekeerd. De correlatie zal echter pas -1 zijn als dat verband perfect lineair is: we kunnen een rechte lijn trekken door als we al onze metingen in een grafiek zouden weergeven.
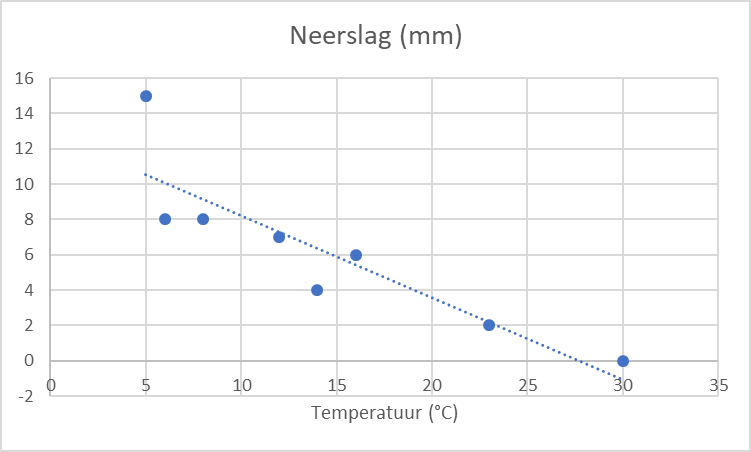
Dit verband kunnen we gebruiken om de neerslag te bepalen. Hoe lager de temperatuur ‘s middags, hoe meer neerslag ‘s avonds. Lineaire relaties en de daarbij horende correlatie, worden regelmatig gebruikt in meteorologie en klimatologie. Meteorologische gegevens zijn immers vaak gerelateerd aan elkaar: een regenbui staat nooit helemaal los van de temperatuur. Een ander voorbeeld is zonneschijn: het aantal uren dat we per dag rechtstreeks zonlicht hebben is ruwweg omgekeerd evenredig met de hoeveelheid neerslag. Eenmaal we zo’n verband hebben, kan dat dus helpen om gegevens te verkrijgen die we niet gemeten hebben. In dit voorbeeld hebben we temperatuur gebruikt om neerslag te bepalen, maar een ander en meer gebruikt voorbeeld is verdamping, dat heel sterk samenhangt met de temperatuur.
Is het echt zo eenvoudig?
Als je nu hoopt dat je met je rekenmachine Frank Deboosere kan overtreffen: ik moet eerlijk toegeven dat dat misschien een beetje kort door de bocht is. Hoewel de basisprincipes die ik hier voorgesteld heb een goed inzicht kunnen bieden in hoe we kunnen beginnen met het weer vanuit een wiskundig perspectief te benaderen, hebben hele generaties onderzoekers ondervonden dat er vaak toch meer bij te pas komt. Elk van de voorbeelden zal bijvoorbeeld enkel maar van toepassing zijn in bepaalde maanden, seizoenen of afhankelijk zijn van weersfenomenen. Het spreekt van zich dat die informatie meegenomen wordt: door extra informatie, zoals de maand of de aanwezigheid van een hoge- dan wel lagedrukgebied mee te nemen, kunnen we de wiskundige modellen scherpstellen.
Op andere momenten lijkt een bepaald model voor de hand liggend, maar hebben we in feite een complexer model nodig. Kijk maar naar het laatste voorbeeld: als het warm is, kan het nog steeds regenen, en zal het vaak zelfs heviger regenen. Denk maar aan zomeronweders! Een lineair verband zal dan niet volstaan. De correlatie die we hierboven gebruikt hebben, ook wel Pearson’s correlatie genoemd, wordt dan minder bruikbaar. Gelukkig is dat niet de enige correlatiemaat!
Laat dat je echter niet tegenhouden om af en toe met een wiskundige blik naar het weer te kijken. Hoe willekeurig het weer soms ook lijkt, we zijn wel degelijk in staat om die willekeur te vatten.




