Drie bekende wiskundige problemen over pizza, plus een grapje dat telt voor 0,14.
1. Neem de pizza met de grotere diameter
Aan de basis van deze uitspraak ligt de vraag: ‘Wat is er meer, één pizza met een diameter van 24 centimeter, of twee met een diameter van 12 centimeter?’ Welnu, de grote heeft een straal van 12 centimeter en dus een oppervlakte van pi maal 12 maal 12 of ongeveer 452 vierkante centimeter. De kleinere heeft een straal van 6 centimeter en dus een oppervlakte van 113 vierkante centimeter. De oppervlakte van de grote pizza is dus zowat 452/113 = 4 maal groter dan de kleinere. Er bestaat trouwens zelfs een online pizzacalculator, die rekening houdt met de korstdiktes van grote en kleine pizza’s.
Aan een pizza met een dubbele straal eet je vier maal zoveel.
2. De pizzastelling
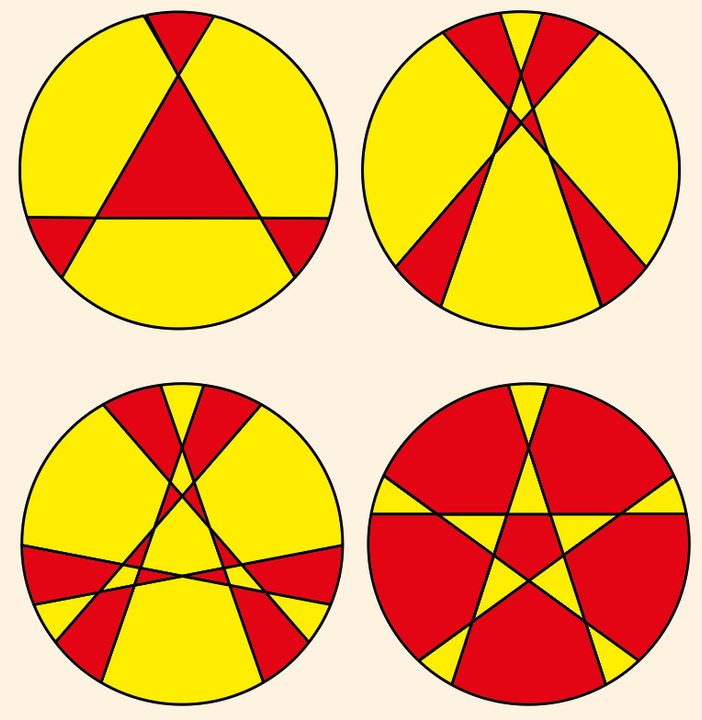
Ze luidt: ‘Als een pizza wordt verdeeld in acht stukken gesneden door eenzelfde punt volgens hoeken van 45 graden, dan is de som van oppervlaktes van de afwisselende stukken gelijk’. Merk op dat een pizzawiel steeds rechte lijnen snijdt van de ene rand naar de andere, dit in tegenstelling tot een taartmes, dat ook punten kan maken zonder de hele taart door te snijden. De stelling is niet vanzelfsprekend. Dat blijkt wanneer we bijvoorbeeld vier stukken snijden doorheen een bepaald punt onder gelijke hoeken van 90 graden.
De stelling werkt ook voor twaalf, zestien … stukken gesneden door eenzelfde punt volgens gelijke hoeken, dus van respectievelijk 30°, 22,5° … maar niet voor twee, vier, zes, tien, veertien … stukken.
Hoewel ze zo’n typische oud-Griekse stelling van tweeduizend jaar geleden lijkt over cirkels en hun onderverdelingen, is deze stelling nauwelijks vijftig jaar oud. Het eigenlijke bewijs van Greg Frederickson aan de Amerikaanse Purdue University, dat ook geldt voor meer dan acht stukken, is zelfs nog geen tien jaar oud.
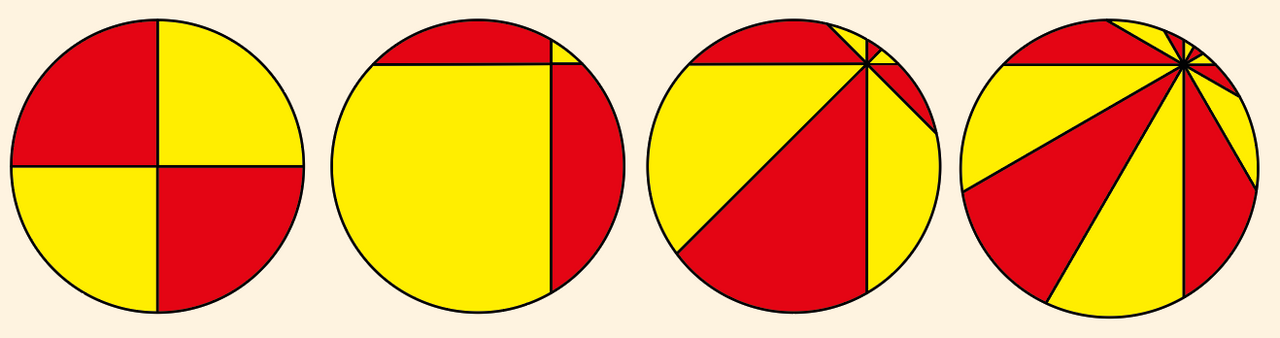
In het eerste geval met vier stukken is de som van de twee rode delen gelijk aan de som van de twee gele, in het tweede geval niet. In het derde geval van acht stukken en het vierde van twaalf stukken is de som van de rode delen wel gelijk aan de som van de gele.
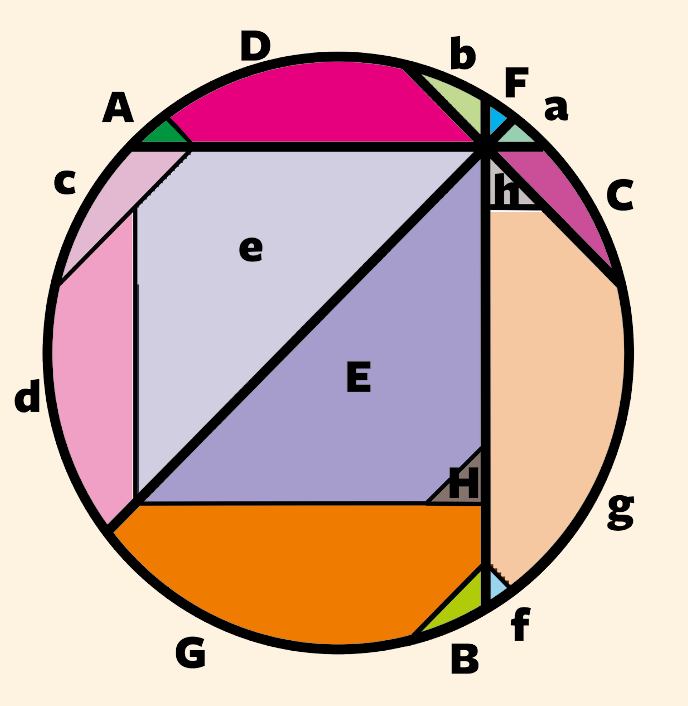
Een illustratie van het bewijs van de pizzastelling voor de gegeven opdeling in acht stukken: de som van de gele delen = a+b+c+d+e+f+g+h = A+B+C+D+E+F+G+H = de som van de rode delen.
3. De luie ober
Een luie pizzaman wil zoveel mogelijk stukken krijgen door zo weinig mogelijk te snijden. Hoeveel stukken zijn dat er, als ze niet noodzakelijk gelijk moeten zijn? Wanneer hij driemaal snijdt, zijn er zes stukken – als hij mooi door eenzelfde punt snijdt dat niet op de rand van de pizza ligt. Het zijn er zeven wanneer zijn drie snijdingen niet door eenzelfde punt gaan. Voor vier snijdingen kunnen het er maximaal elf zijn, voor vijf zestien. Enzovoort: de getallen van de ‘lazy caterer’ zijn 1, 2, 4, 7, 11, 16, 22, 29, 37, 46, 56, 67, 79, 92, 106 … Je kan dit desnoods ‘proefondervindelijk’ nagaan.
Het maximale aantal stukken waarin een pizza kan worden versneden door drie-, vier-, vijf- of zesmaal te snijden.
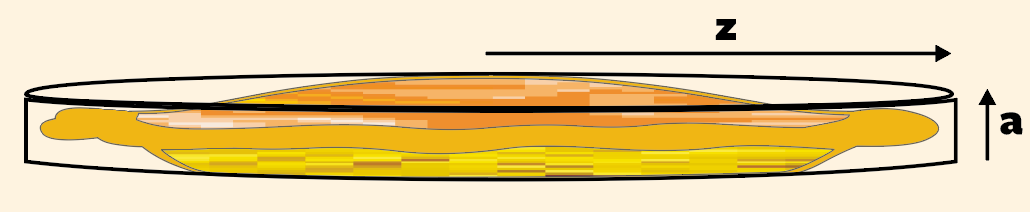
0,14. Wat is het volume van een cilinder met straal z en hoogte a?
Het antwoord is een standaard nerd-grapje: pi maal straal z maal straal z maal a of pi.z.z.a.