Het wiskundetijdschrift Pythagoras bestaat zestig jaar. Dat wordt gevierd met een boek vol doordenkers. Ook wiskundige Dirk Huylebrouck waagde zich eraan. 'Ik voelde mijn hersenen opnieuw kraken alsof ik jong was.'
De Dikke Van Dale is één van de belangrijkste woordenboeken in de Nederlandse taal. In tijden van spellingcheckers vermindert zijn belang snel en dus ook zijn bekendheid. Hij zal de tand des tijds misschien niet doorstaan, in tegenstelling wellicht tot de Dikke Pythagoras, een boek met meer dan zeshonderd wiskundige vraagstukken, waarvan sommige al duizenden jaren oud zijn. In het boek kregen ze natuurlijk wel een modern jasje.
Eén van de auteurs zal de Eos-lezer bekend voorkomen, omwille van zijn blogs en artikels: Paul Levrie, een wiskundige verbonden aan de faculteit Toegepaste Ingenieurswetenschappen van de UAntwerpen. Hij werkt al lang mee aan het tijdschrift Pythagoras, een begrip in wiskundig Nederland en Vlaanderen. Samen met Jan Guichelaar, het oudste lid van de redactie van het tijdschrift, en Roosmarij Vanhommerig, de hoofdredacteur, bundelde hij in het boek de beste doordenkers die de voorbije zestig jaar in Pythagoras zijn verschenen, doorspekt met talloze leuke wist-je-datjes.
Toen ik Paul naar zijn lievelingsvraagstuk vroeg, koos hij ‘het nummertje 148’. Boven het vraagstuk stonden een passer en drie bolletjes, waarvan er twee zwart waren. Die wezen respectievelijk op het soort vraagstuk (een meetkundig, in dit geval) en op de moeilijkheidsgraad: ‘In de figuur zie je een vierhoek. Twee lijnen, die door de middens van twee overstaande zijden gaan, delen de vierhoek in vieren. Van drie stukken is de oppervlakte gegeven. Wat is de oppervlakte van het vierde stuk?’
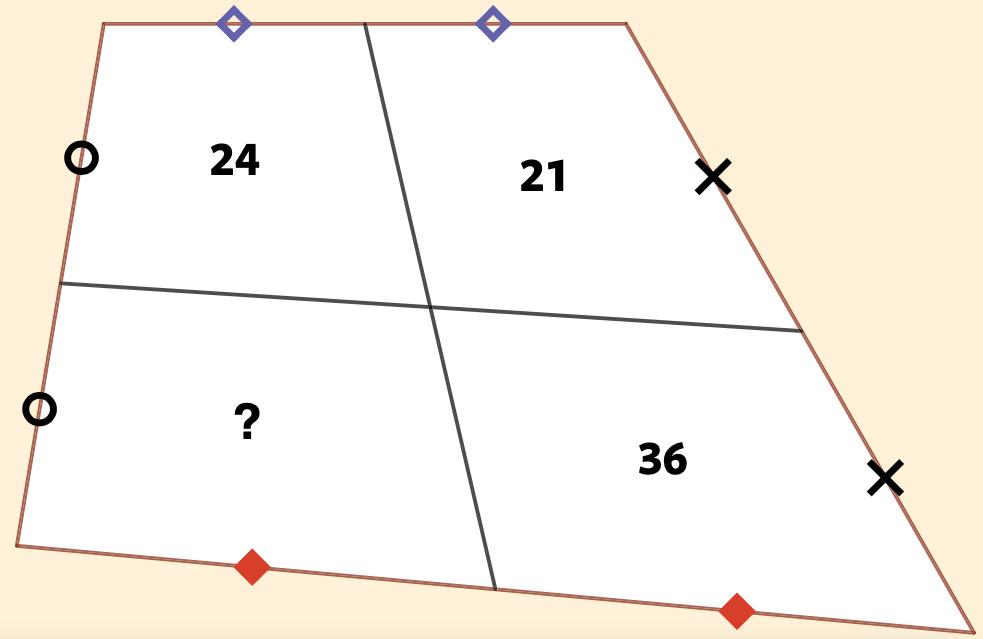
Ik hoor de lezer denken: ‘Een wiskundige lost zoiets toch onmiddellijk op?’ Maar ik ben niet te beroerd om toe te geven dat ik er zelf een hele kluif aan had! Ik voelde mijn hersenen opnieuw kraken alsof ik jong was. Een tip: je hebt géén formules nodig voor de oppervlakte van een vierhoek, en ook niet een of andere stelling over vierhoeken. Het vraagstuk kan met één tekening worden opgelost.
Ik vroeg aan Paul waarom hij dit vraagstukje uitkoos. Een van zijn redenen was dat het een interessante veralgemening heeft: ‘Neem een vierhoek,’ zei hij, ‘en verdeel elk van de zijden in een even aantal gelijke delen. Verbind die punten met behulp van een lijn met het overeenkomstige punt op de tegenoverliggende zijde. Als je nu het resultaat inkleurt met een dambordpatroon, dan is de totale oppervlakte van de witte velden gelijk aan de totale oppervlakte van de zwarte.’

Een goede vondst, inderdaad, en ze illustreert ook hoe je met de nodige creativiteit zelf een stelling kunt bedenken.
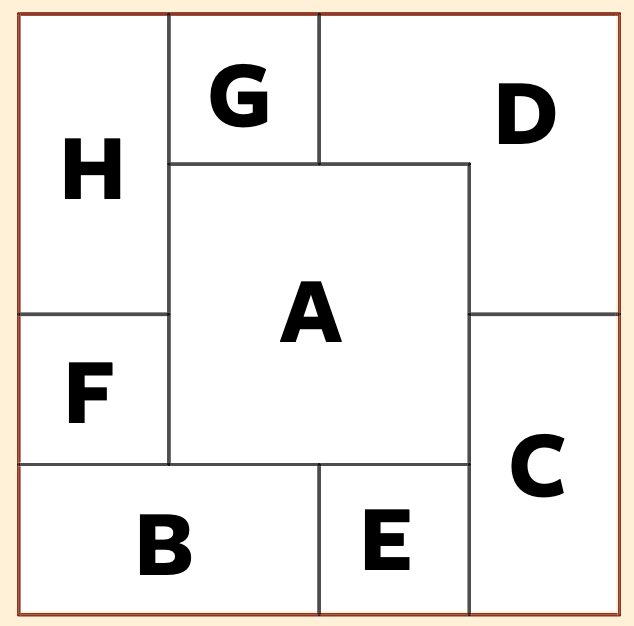
Niet alle puzzels zijn meet- of rekenkundig van aard. Zo zijn er ‘raadsels’ die een andere, speciale manier van redeneren vergen (nummer 168 in het boek): ‘Acht vierkante velletjes papier, allemaal even groot, worden een voor een op elkaar gelegd, elkaar steeds gedeeltelijk overlappend. Het resultaat, een groot vierkant, zie je in de figuur. Kun je de velletjes papier in de correcte volgorde opnoemen, van het bovenste tot en met het onderste velletje?’
Het boek illustreert dus ook mooi dat wiskunde ruimer is dan gemeenzaam aangenomen. En, oh ja, zelfs elk paginanummer bevat een uitdaging. Zo staat bij het paginanummer 94 de combinatie – 1 × 1 + ((–2/2 + 3) × 3 + 4) × 4 + 55 en wordt aan de lezer gevraagd om een andere oplossing te vinden, door enkel de cijfers 1, 1, 2, 2, 3, 3, 4, 4 in die volgorde te gebruiken. Er zijn 299 genummerde pagina’s, en dus 299 extra puzzels.
De oplossingen van de raadsels in deze column, vind je onderaan deze pagina.
Oplossing: De vier vierhoeken kunnen elk worden verdeeld in twee driehoeken, zodat de resulterende acht driehoeken vier paren vormen, die twee aan twee dezelfde oppervlakten hebben (gelijke basis en gelijke hoogte). De gevraagde oppervlakte is (a+d) = (a+b) + (c+d) – (b+c) = 24 + 36 – 21 = 39.
Vellen: A, D, G, H, F, B, E, C; pagina: 1 × 1 + 2 × 23 + 3 + 44 (bijvoorbeeld).