Je hebt intussen ongetwijfeld de grafiek gezien die massaal gedeeld wordt onder de slogan 'flatten the curve'. Bloggers Simon Telen en Andreas Van Barel leggen de wiskundige basis van het model uit.
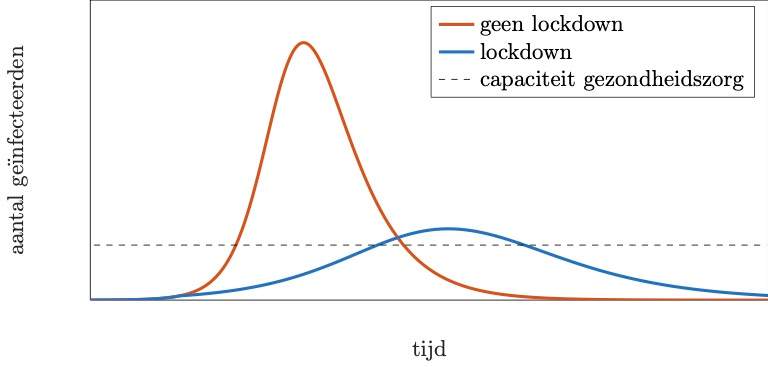
Deze grafiek, die men soms de 'coronacurve' noemt, toont het aantal besmette mensen als functie van de tijd. Als we geen actie ondernemen volgen we de rode curve. Te veel mensen worden dan kort na elkaar ziek waardoor de capaciteit van de gezondheidszorg overschreden wordt. Het idee van social distancing, teleworking en andere dergelijke maatregelen is om de verspreiding van de ziekte te vertragen. Dit resulteert in de blauwe curve. Minder mensen moeten dan tegelijkertijd opgenomen worden in de ziekenhuizen zodat de meeste (en in het beste geval alle) patiënten toch een plaats zullen hebben. Maar hoe komt men eigenlijk tot deze grafiek? Waarom stijgt het aantal besmettingen eerst zo snel? Waarom zou dit aantal uiteindelijk dalen, als het virus toch zo besmettelijk is?
Om deze vragen te beantwoorden, bespreken we een sterk vereenvoudigd model dat de verspreiding van infectieziekten beschrijft. Dit model, dat bekend staat als het SIR-model, deelt de bevolking op in drie groepen:
1. Groep S van vatbare personen. Zij hebben het virus nooit gehad maar kunnen eventueel besmet worden.
2. Groep I van geïnfecteerde personen. Zij hebben het virus en kunnen personen uit groep S besmetten.
3. Groep R van genezen of gestorven personen. Zij hadden de ziekte, maar zijn intussen genezen of gestorven. Zij kunnen de ziekte niet opnieuw krijgen. We veronderstellen dus dat als je geneest, je immuun wordt voor de ziekte.
De namen van de groepen komen van het Engelse 'susceptible', 'infective' en 'recovered'.
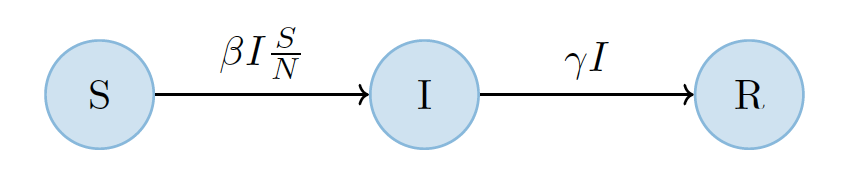
Schematisch kunnen we het SIR-model voorstellen als volgt.
Om te begrijpen hoe de coronacurve uit het model voortkomt, moeten we preciseren hoe snel de mensen uit groep S terechtkomen in groep I, en mensen uit I uiteindelijk in groep R. Volgens het SIR-model gebeurt de overgang van S naar I sneller wanneer er meer mensen in groep I zitten. Inderdaad, hoe meer mensen er al ziek zijn en dus anderen kunnen besmetten, hoe sneller de ziekte zich verspreidt. Hoe gemakkelijk het juist is voor een besmet persoon om het virus door te geven wordt verder bepaald door een parameter die we $\beta$ zullen noemen. Deze parameter geeft aan hoeveel andere mensen er per dag door één geïnfecteerde persoon blootgesteld worden aan de ziekte. Niet iedereen die blootgesteld wordt is echter vatbaar voor de ziekte. Voor mensen die de ziekte al hebben (groep I) verandert er niets. Mensen die de ziekte ooit al gehad hebben (groep R) zijn volgens ons model immuun. Alleen de groep S is vatbaar, en zij maken slechts een fractie van de totale bevolking uit. Daardoor zullen er voor elke besmette persoon niet gemiddeld $\beta$ personen per dag besmet worden, maar slechts $$\beta \times \frac{\text{aantal vatbare personen}}{\text{aantal mensen in de bevolking}}.$$ We concluderen dat er elke dag
$$ \beta \times \text{aantal geïnfecteerde personen} \times \frac{\text{aantal vatbare personen}}{\text{aantal mensen in de bevolking}}$$
nieuwe besmettingen plaatsvinden. Gebruiken we de korte notatie $S$, $I$, en $R$ voor het aantal vatbare, geïnfecteerde en immune personen en de letter $N$ voor het aantal mensen in de bevolking, dan geeft dit het getal $\beta I \frac{S}{N}$.
De tweede overgang is die van I naar R. Hoe snel mensen genezen of sterven hangt uiteraard af van ziekte tot ziekte. Een tweede parameter $\gamma$ geeft aan welk deel van de besmette mensen I per dag ofwel geneest ofwel sterft. Elke dag komen er dan
$$
\gamma \times \text{aantal geïnfecteerde personen} = \gamma I
$$
individuen uit groep I in groep R terecht. Met deze informatie kunnen we de schematische voorstelling van het SIR-model vervolledigen tot
Gebruik makend van dit eenvoudig model kunnen we met de computer de evolutie van $S$, $I$ en $R$ berekenen. Daarvoor hebben we wel waardes nodig voor $\beta$ en $\gamma$. Op dit moment is er echter weinig betrouwbare data beschikbaar, zodat we $\beta$ en $\gamma$ voor het coronavirus niet precies kennen. In het onderstaande resultaat hebben we enkele redelijke waardes voor deze parameters gekozen.
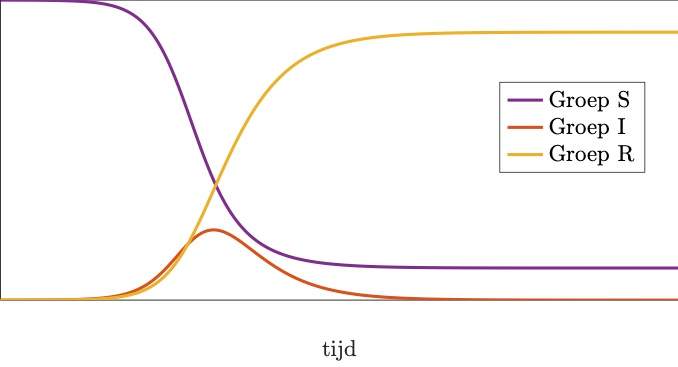
De rode curve hier geeft $I$, en is exact dezelfde als de rode curve uit de eerste figuur. Hij ziet er wat kleiner uit omdat $S$ en $R$ nu ook op de grafiek staan. Laat ons nu het verloop van $S$, $I$ en $R$ verklaren aan de hand van de schematische voorstelling van het SIR-model. Vanuit de groep S is er enkel een pijl die weg wijst. Dit betekent dat het aantal mensen dat vatbaar is voor de ziekte enkel kan dalen in de tijd. Aan de andere kant van het diagram maken we dezelfde redenering: er is enkel een pijl die naar R wijst, dus het aantal immune personen zal steeds toenemen. Voor de groep I is er zowel een binnenkomende als een uitgaande pijl. In het begin van de epidemie, wanneer er nog niet veel mensen besmet zijn (de groep I is klein) en veel mensen vatbaar zijn (de groep S is groot), zal de overgang van S naar I veel sneller gebeuren dan die van I naar R. Met andere woorden, de binnenkomende pijl wint het van de uitgaande pijl en het aantal personen in groep I stijgt. Initieel gebeurt deze stijging sneller en sneller. Dit is de fase van de epidemie waarin er sprake is van een exponentiële groei van het aantal besmettingen. Gedurende deze fase groeit de groep I en verkleint de groep S. Na verloop van tijd zijn er nog zo weinig personen vatbaar dat het moeilijk wordt voor het virus om nog nieuwe mensen te infecteren. Stilaan begint de uitgaande pijl van I naar R het te winnen van de binnenkomende pijl. Het aantal geïnfecteerde personen neemt dan terug af. Op die manier zien we de coronacurve tevoorschijn komen.
Aangezien de parameter $\beta$ modelleert hoe gemakkelijk het is voor het virus om zich te verspreiden, is dit net de parameter die we als maatschappij kunnen beïinvloeden. In onze simulaties beschouwen we een populatie van 11 miljoen personen, wat ongeveer het aantal Belgen is. We nemen aan dat er 100 dagen nadat de ziekte zich begint te verspreiden 'lockdown maatregelen' worden doorgevoerd. Hierdoor verlaagt de waarde van $\beta$ en toont de curve een ander, vlakker verloop. Dit kan je zien op onderstaande animatie.
Het verlagen van $\beta$ zorgt ervoor dat de piek van de curve veel lager blijft. De capaciteit van de ziekenhuizen wordt dan minder lang, minder sterk, of hopelijk zelfs niet overschreden. De patiënten worden meer 'verspreid' in de tijd. De piek gebeurt dus ook pas later. We kunnen ook nakijken wat de invloed is van de lockdown op het aantal vatbare, besmette en immune personen. Met behulp van een lichtjes aangepast model kunnen we de groep R verder opsplitsen in gestorven en genezen mensen. Zo bekomen we onderstaande animatie, waarin voor verschillende waarden van $\beta$ het aantal genezen, vatbare, besmette en gestorven personen wordt weergegeven gedurende 1 jaar.
Merk op dat hoe meer we $\beta$ kunnen verkleinen door de lockdown richtlijnen strict na te leven, hoe minder mensen er uiteindelijk besmet zullen worden door het virus en hoe kleiner het verwachte aantal sterfgevallen. We concluderen: 'blijf in uw kot'!
Wie genteresseerd is in meer details kan ons iets uitgebreider, Engelstalig artikel hier vinden.
