Sommige wiskundige problemen lijken op het eerste gezicht heel eenvoudig, maar zijn dat helemaal niet.
Doorheen mijn jaren als columnist werd ik al eens benaderd door een lezer die me een wiskundig vraagstuk voorlegde waarmee hij of zij al een tijd had liggen worstelen. Telkens vond ik het moeilijk om vooraf te weten of het vraagstuk de tijd zou lonen of niet. Sommige wiskundige problemen lijken ogenschijnlijk zeer eenvoudig, maar zijn dat helemaal niet. Andere problemen dienen zich erg complex aan, terwijl ze makkelijk vallen op te lossen.
Beschouw bijvoorbeeld een geit die alles eet wat in haar bereik ligt. Ze is vastgemaakt aan een touw, waarvan het uiteinde aan een paaltje vastzit op de rand van een cirkelvormig grasperk. Als het touw kort is, kan de geit niet veel eten. Als het touw daarentegen minstens zo lang is als de diameter van het grasperk, dan kan ze alles kaalvreten. De vraag is nu: hoe lang moet dat touw zijn opdat de geit precies de helft van alle gras zou opeten?

Dat moet makkelijk op te lossen zijn. Moeten we niet alleen maar de formule voor de oppervlakte van een cirkel – pi maal straal maal straal – nemen, en die aanpassen voor dit van een stuk van een cirkel, door het afgegraasde deel in stukken van cirkels op te splitsen (zoals gesuggereerd door de stippellijn)? Dat klopt, en toch krijgen we het vraagstuk niet opgelost zonder de hulp van een computer. Tenzij we ellenlange numerieke berekeningen met de hand zouden willen uitvoeren. Ik heb er in elk geval al menig opschepper die snoefde met zijn wiskundige kennis mee zoet gehouden. Voor wie zelf ook last heeft van wiskundige allesweters, de oplossing is: r = 1,15872847…
Anderzijds zijn er ook vraagstukken die moeilijk lijken, maar eigenlijk een erg elegante oplossing hebben. Zoals het volgende. Gegeven is een vierkant ABCD met zijde 1, waarin een halve cirkel is getekend met diameter 1 en als middelpunt het midden M van een van de zijden – stel, AD. De raaklijn aan die cirkel vanuit een hoekpunt van het vierkant – stel, B – ligt niet op die cirkel. Gevraagd is dan hoe lang het stuk is van die raaklijn, vanaf het hoekpunt B van het vierkant tot het punt E, waar de raaklijn de tegenoverliggende zijde CD van het vierkant snijdt. Met andere woorden, hoe lang is BE?
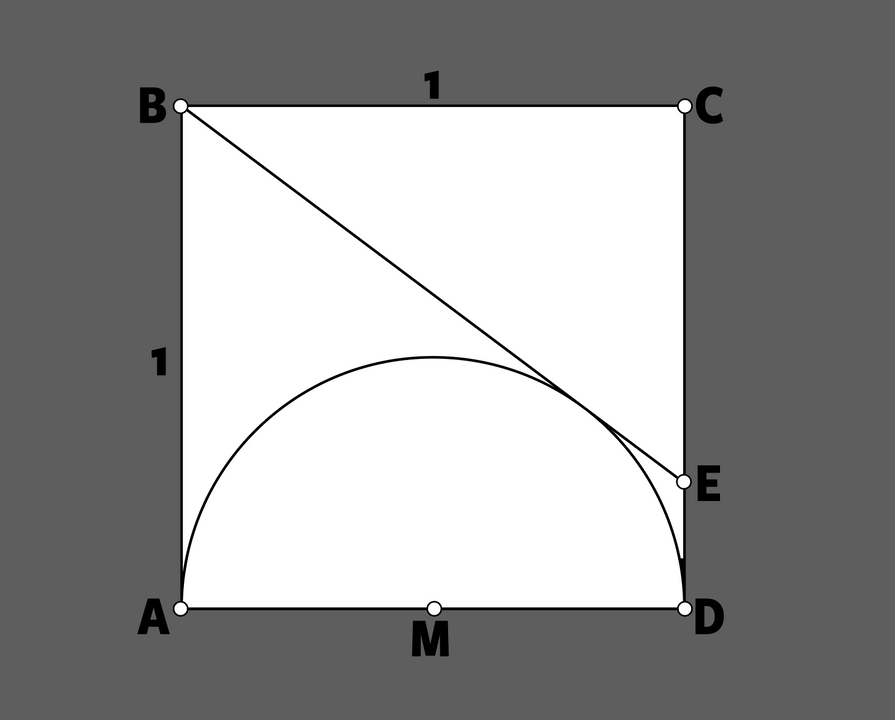
We hebben geen hogere wiskunde nodig om het vraagstuk op te lossen. Het kan zelfs zonder de stelling van Pythagoras. Sterker nog: het kan worden opgelost zonder ook maar een formule op te schrijven. Je kan het oplossen in de kantlijn van een Eos, in de wachtkamer van de dokter of kapper.
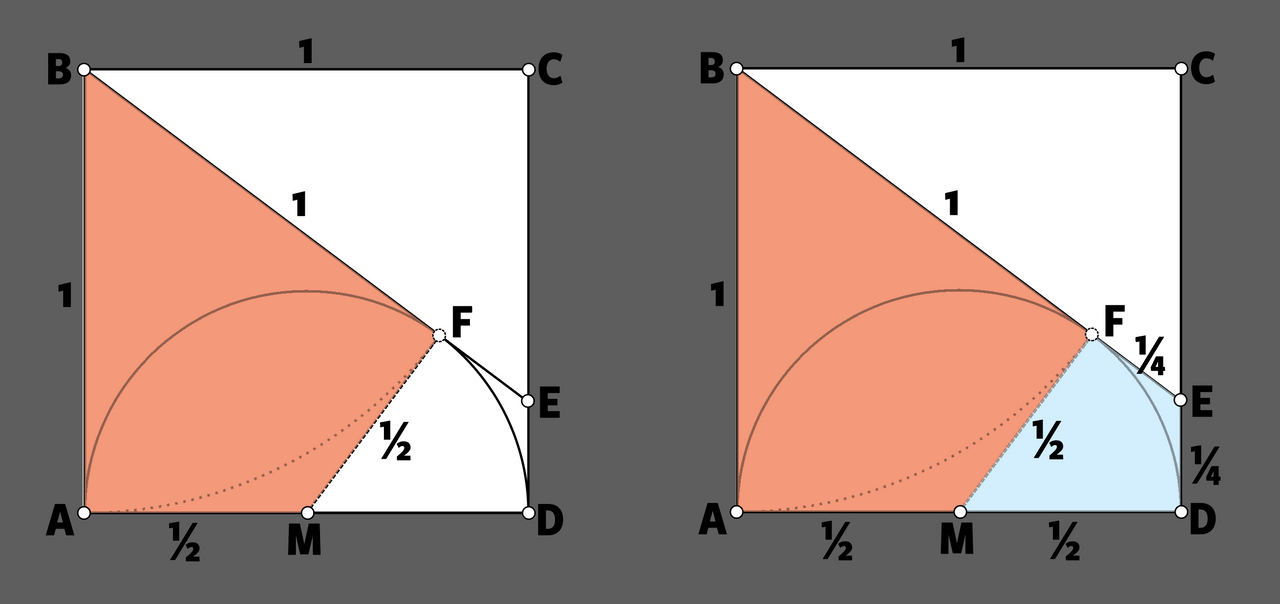
Het antwoord, dan. We beschouwen een cirkelboog met middelpunt B en straal 1 (de boog in stippellijnen op de tekening). Die snijdt de halve cirkel met middelpunt M in het raakpunt F, wat aanleiding geeft tot de rode vierhoek BFMA. Hierin is BA gelijk aan 1, want de zijde van het vierkant meet 1. BF is dus ook gelijk aan 1. We beschouwen nu de blauwe vierhoek MFED. Hij heeft dezelfde vorm als de vierhoek BFMA, alleen zijn zijn zijden allemaal half zo groot als de overeenkomstige zijden van BFMA. Omdat AM de lengte 1/2 heeft en FE hiervan de helft is, is de lengte van FE dus 1/4. Dus is BE = 1 + 1/4 = 5/4 = 1,25. Of hoe je met een beetje gezond wiskundig verstand een flink eind ver raakt.