Ieder kind in Japan kan een kraanvogel vouwen – de eerste gepubliceerde vouwinstructies voor het figuurtje dateren al van 1797. Origami is een gevestigde waarde geworden in speelgoed, huis- en tuindecoratie, rituelen, creatieve workshops of didactische projecten.
Maar de laatste dertig jaar zien we toch een opvallende evolutie in de origamiprestaties. Soms worden uit één blad papier evenveel plooien gevouwen als een senbazuru, een verzameling van duizend papieren kraanvogels. Kijk maar naar de wonderlijke creaties van de hedendaagse origamist Robert Lang. Met één blad papier en zonder schaar of lijm creëert hij een schitterende schorpioen.

Nochtans is er in de loop der eeuwen niets veranderd aan de techniek, die in wezen niets meer om het lijf heeft dan vouwen. Iemand als Lang twijfelt niet over de oorzaak van de recente hoge vlucht die origami heeft genomen. Volgens hem heeft het alles te maken met de bemoeienis van wiskunde.
Intussen bestaat er zoiets als wiskundig origami, dat de axioma’s en basiseigenschappen van papiervouwen onderzoekt. En er is computationeel origami, dat algoritmes zoekt om het ontwerp van een vouwpatroon te automatiseren voor een gegeven doelobject. En om, als het even kan, een vouwprocedure voor dat patroon op te stellen. Een vouwpatroon is een diagram met plooilijnen dat aangeeft welke plooi je als vallei en welke je als berg moet vouwen (zie kaderstuk ‘Vouwpatronen’).
De wiskundige en computationele ontplooiing van origami hebben we te danken aan protagonisten als Martin Gardner, Erik Demaine, Kōryō Miura, Thomas Hull, Ileana Streinu en Robert Lang. Maar eigenlijk gaat de grootste verdienste voor de recente origami-explosie naar wiskunde die al veel vroeger werd ontwikkeld en die deze bollebozen gretig toepassen. Denk aan gebieden als grafentheorie, polytopentheorie, computationele meetkunde, de theorie van vlakke stapelingen en betegelingen, kinematica, starheidsstudie en zelfs statistische mechanica.
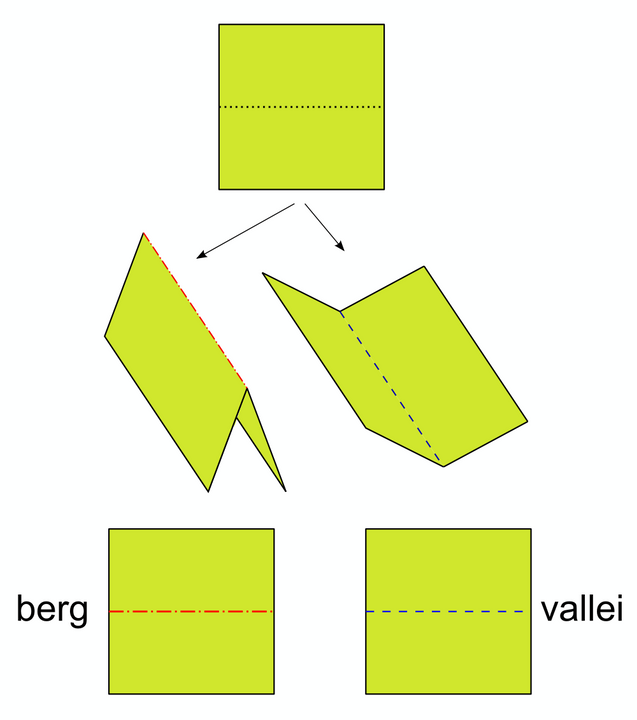
Een vouwpatroon is een tekening op een vierkant of in een andere convexe veelhoek (meestal plat) met knooppunten (inwendig of op de rand) die verbonden zijn door plooilijnen. Het is wat je ziet wanneer je het origamiresultaat weer openvouwt.
In dit diagram onderscheiden we twee soorten plooilijnen: bergplooien en valleiplooien (rood en blauw in de figuur).
In computationele origami beschouwt men de opdracht als volbracht zodra dat vouwpatroon (met rode en blauwe plooien) berekend is.
Een vouwpatroon met voor iedere plooi de keuze tussen ‘berg’ of ‘vallei’ is pas bruikbaar wanneer de uitvoering ervan tot een perfect platte origamibasis leidt. Dat is aangenomen dat er 100 procent correct gevouwen wordt met oneindig dun papier en oneindig dunne plooien.
Vervolgens kunnen de flappen van deze platte origamibasis gelift worden tot het gewenste 3D-object. Om geldig te zijn, moet een vouwpatroon aan een aantal basisregels voldoen. Maar deze regels geven helaas geen garantie op een geldig patroon, want dat is niet zo gemakkelijk na te gaan. Publicaties uit 1996 (Bern en Hayes) en uit 2018 (Akitaya, Demaine, Horiyama, Hull, Ku en Tachi) hebben inderdaad aangetoond dat er in het algemene geval geen efficiënt algoritme bestaat om de geldigheid van een gegeven vouwpatroon te controleren.
Nieuw gereedschap
Nieuwe wiskundige inzichten en software om patronen op aanvraag te berekenen, leidden recent tot oplossingen om grote telescooplenzen of zonnepanelen op te vouwen en de ruimte in te schieten, waarna ze zichzelf openen. De pas gelanceerde James Webb Space Telescope wordt niet voor niets NASA’s origamitelescoop genoemd.
Er zijn nog meer voorbeelden. Aan Harvard University ontwerpen onderzoekers gelachtige robots die in staat zijn om zichzelf te ontvouwen, een taak uit te voeren en daarna op te lossen of zichzelf te recyclen. En op veel kleinere schaal zijn wetenschappers van Stanford University erin geslaagd om op afstand bestuurbare opgevouwen robots te ontwikkelen die een bepaald medicijn naar de gewenste plaats in het menselijke lichaam kunnen transporteren. Origami kan dus levens redden!
De reden om computationele origami en vouwtechnologieën te ontwikkelen is niet altijd louter artistiek of pragmatisch. Soms is het de ontwikkelaar puur om het recreatieve te doen. Kijk maar naar die ene goocheltruc van Harry Houdini of de onschuldige puzzelopdracht van Martin Gardner. Al vloeide daaruit wel de fameuze vouw-en-knipstelling voort (zie kaderstuk). Op zijn beurt leidde dat tot mogelijkheden voor een snellere productie bij lasercuttoepassingen.
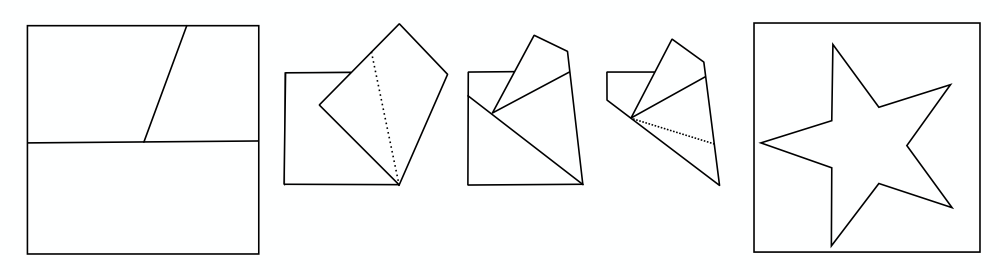
Een mooi voorbeeld van hoe eenvoudig vermaak kan leiden tot wiskundige ontwikkelingen is het vouw-en-knipprobleem. De bekende illusionist Harry Houdini beschreef in zijn boek Paper Magic uit 1922 hoe je uit een vierkant stuk papier met één rechte knip een vijfpuntige ster kan knippen. Hiernaast (bovenaan) zie je de bijbehorende figuur, waarbij je moet knippen volgens de stippellijn in de voorlaatste figuur rechts.
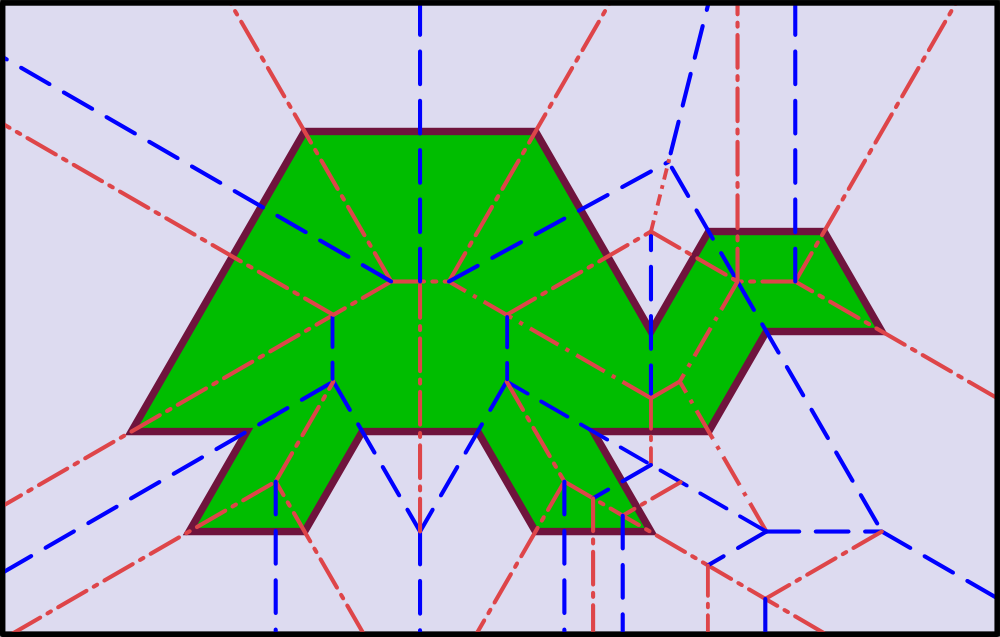
In 1999 was er dan de vouw-en-knipstelling, die zegt dat je een vouwpatroon kan vinden om dat te doen voor eender welke figuur met rechte zijden. Hiernaast zie je een tekening van een schildpad en welke vouwen je moet maken om die met een rechte snee uit te knippen.
Het lijkt misschien onwaarschijnlijk dat dit altijd kan. Daarom willen we de lezer even zelf aan het werk zetten met de bedoeling te laten aanvoelen wat erbij komt kijken. We vertrekken telkens van een vierkant blad papier. Teken op dat blad een figuur zoals je onderaan ziet.
Probeer nu het vierkant zo op te vouwen zodat je met een schaar met één rechte knip de figuur kan uitsnijden. Het kan dus altijd! De auteurs van de stelling (Erik Demaine, Martin Demaine en Anna Lubiw) leverden ook het algoritme om het vouwwerk te maken.

De origamioogst bevat meer dan speelgoed, rituelen, kunst of technologische toepassingen. Er is namelijk ook een fundamentele terugkoppeling naar wiskunde. Origami is hoe langer hoe meer een nieuw gereedschap in onze wiskundekist, naast calculus, algebra, klassieke meetkunde, enzovoort. Het is zelfs zo dat sommige meetkundige constructies, zoals het verdelen van een willekeurige hoek in drie gelijke delen, niet zuiver mogelijk zijn met passer en liniaal, maar wel met vouwen.
Ook de algebra moet gefrustreerd toegeven dat ze geen formules heeft om bepaalde veeltermvergelijkingen op te lossen, terwijl dat wel lukt met een geschikte vouwstrategie. Anekdotisch maar exemplarisch is de origamioplossing die in 2005 gevonden werd om het spel Countdown optimaal te spelen: probeer zo dicht mogelijk bij een gegeven getal te komen met behulp van basisbewerkingen op een gegeven rijtje getallen.
Sinds het begin van deze eeuw probeert computerwetenschapper Jeremy Gibbons uit Oxford om origami op een structurele manier in algoritmes te gebruiken. Zijn werk gaf aanleiding tot een nieuwe manier om recursieve functies te coderen: origamiprogrammeren.
Origami in outer space
In het dagelijks leven dient vouwen een praktisch nut: voorwerpen optimaal opbergen en eenvoudig vervoeren. Vandaar ook de zoektocht naar eenvoudige en snelle vouwpatronen, die achteraf ook gemakkelijk kunnen worden ontvouwd.
Gewoonlijk zijn we daarbij weinig geïnspireerd. Of het nu landkaarten of handdoeken betreft: we gebruiken standaard twee loodrecht op elkaar staande vouwrichtingen, zodat de plooilijnen van het patroon een rechthoekig rooster vormen. Maar dat klassieke rechthoekige vouwen vereist veel bewegingen. En dus ook veel energie. Dat is een nadeel als we die operatie elektronisch of motorisch willen automatiseren.
En als we hetzelfde rechthoekige vouwpatroon meermaals moeten toepassen, wordt het materiaal bovendien zwaar belast. Denk maar eens terug aan de gescheurde plooien in de oude wegen- of fietskaarten uit de tijd waarin we nog geen gebruik maakten van satellietnavigatie.
Soms worden uit één blad papier evenveel plooien gevouwen als een verzameling van duizend papieren kraanvogels
Eind jaren 1970 ontdekte de Japanse astrofysicus Kōryō Miura een nieuw opvouwpatroon, met parallellogrammen waarvan de hoeken net 6° afwijken van 90°. Die afwijking van het rechthoekige patroon ontlast het bladmateriaal aanzienlijk. Verder worden de parallellogrammen niet gebogen tijdens de vouwprocedure. Daardoor kan je ze uit star materiaal fabriceren.
Bijkomend voordeel van Miura-ori of de Miura-vouw: ze verbeteren de materiaalsterkte van het onderliggende blad significant. Maar de grootste troef is ongetwijfeld dat er slechts één vrijheidsgraad aanwezig is. Voor het automatisch open- en toevouwen heb je dus maar één motor nodig.
Via Miura belanden we opnieuw bij de ruimtevaart. In 1985 demonstreerde Miura, die toen directeur was van het instituut voor kosmologie en astronautica in Tokio, hoe je grote membranen compact kan vervoeren voor een ruimtereis en ze op afstand automatisch laten ontvouwen. De techniek werd in 1996 effectief toegepast bij de zonnepanelen voor een satelliet van JAXA, de Japanse pendant van NASA.
De Miura-oritechniek werd recent nog gebruikt voor het Japanse Sprout-project (Space Research on Unique Technology). Nanosatellieten worden daarbij volledig opgevouwen de ruimte in gestuurd.
Miura-ori heeft trouwens niet alleen toepassingen in de ruimtevaart. De techniek werd ook al gebruikt om batterijen te ontwerpen met in stapels gevouwen hydrogel-elementen, die volgens het principe van de sidderaal elektriciteit opwekken. Sinds 2014 gebruikt de Amerikaanse fysicus Arthur Evans Miura-patronen met sporadische foutjes om statistisch-mechanische eigenschappen van gassen en vloeistoffen te modelleren. En biotechnologen bedienen zich van de techniek om het openbloeien van gebladerte te modelleren.
Algoritmes en automatisering
Het huwelijk tussen origami en wetenschap houdt tot op de dag van vandaag spetterend stand. De liefde komt dan ook van beide kanten. Origami bood ons al heel wat technologische toepassingen. En omgekeerd maakten wiskundige eigenschappen en computeralgoritmes vouwkunstwerken museumwaardig.
Eén wetenschapper is er zelfs in geslaagd om als voltijds origamist zijn boterham te verdienen. In 2001 nam de Amerikaanse Robert Lang afscheid van een succesvolle ingenieurscarrière om zich volledig toe te leggen op origami. Vandaag wordt zijn advies gevraagd voor allerlei hoogtechnologische toepassingen, zoals ontwerptests van airbags of plooitechnieken om – daar zijn ze weer – telescopen de ruimte in te sturen.
Als (co)auteur van 21 boeken is Lang een veelgevraagde spreker, en zijn vouwcreaties zijn erg gewild. En dan hebben we nog niets gezegd over de lucratieve opdracht die hij kreeg van Mitsubishi voor een prestigieuze promotiefilm.
Het ‘origami op aanvraag’ van Lang begint met een tekening van het gewenste resultaat. Met software die hij daartoe heeft ontworpen, maakt hij vervolgens een skeletvoorstelling. Dan komt de moeilijkste stap: het ontwikkelen van een origamipatroon met plooilijnen. Op het skeletmodel wordt daarvoor een cirkelconfiguratie berekend. De correcte vouwing van de plooien levert een platte origamibasis op, die je uiteindelijk kan openen tot de gewenste 3D-figuur.
In 1999 publiceerde de toen achttienjarige Canadese computerwetenschapper Erik Demaine een algoritme dat ieder denkbaar 3D-object kon vouwen met één blad papier, zonder lijm of schaar. Het was een mijlpaal op het gebied van computationeel origami. Al bleek het belang van het algoritme vooral theoretisch van aard. Het algoritme gebruikte een lange strook papier met heel veel plooien – niet zo handig voor praktische uitvoeringen.
Later ontwikkelde ook de Japanner Tomohiro Tachi een computerprogramma voor de automatisering van origami. Dat had weliswaar niet de universele kracht van Demaines algoritme, maar het was wel praktisch uitvoerbaar. In 2008 maakte Tachi zijn programma beschikbaar onder de naam Origamizer.
Uiteindelijk bundelden Demaine en Tachi de krachten. In 2017 stelden ze een algoritme voor dat een origamipatroon berekent voor eender welk 3D-voorwerp, deze keer met zo weinig mogelijk plooien en met een vierkant blad papier met normale proporties. Een ronduit verbijsterende prestatie.
De computer levert weliswaar de oplossing voor ieder willekeurig origamiprobleem, maar hij doet dat in de vorm van een berg-valleiplooipatroon. Je bent op jezelf aangewezen om volgens dat patroon tot een plat basismodel te komen. Ook voor het opkrikken van de flappen van het platte model tot een 3D-object blijkt onze menselijke handigheid nog steeds een vereiste.
De klassieke origami-ambachtelijkheid zal wellicht nog enige tijd onmisbaar zijn. Zowel voor artistieke als technologische toepassingen.





