Wist je dat 

• $\ldots$  je vandaag taart (`pie') moet eten, of nog beter: trakteren met taart op je werk?
• $\ldots$  het getal $\pi$ de verhouding geeft van de omtrek van een cirkel tot de diameter, maar ook de verhouding van de oppervlakte van die cirkel tot het kwadraat van zijn straal?
• $\ldots$  sinds 26 november 2019 dankzij Unesco:

• $\ldots$  het getal $\pi$ tot op 500 cijfers na de komma gelijk is aan:

• $\ldots$ pas op het einde van de 16de eeuw bovenstaande notatie voor decimale getallen, met de decimale punt (of komma), in onze contreien werd ingevoerd? Voordien werd het getal 3.1415 geschreven als $$3 \frac{1415}{1000}$$ waardoor het rekenen met cijfers na de komma niet eenvoudig was. Simon Stevin (1548-1620), onze Brugse wiskundige, voerde een nieuwe notatie in die het rekenen ermee eenvoudiger maakte (links op de figuur). Het eerste decimale punt treffen we aan in een boek van Christophe Clavius (1538-1612) uit 1593, rechts zie je een detail:

• $\ldots$  waarschijnlijk de eerste keer de notatie $\pi$ gebruikt werd voor deze verhouding in het boek Synopsis Palmariorum Mathesos (1706) (vrij vertaald: een nieuwe inleiding tot de wiskunde) van ene William Jones (1675-1749)? De Zwitserse wiskundige Leonhard Euler (1707-1783) zorgde voor de verdere verspreiding van deze notatie.

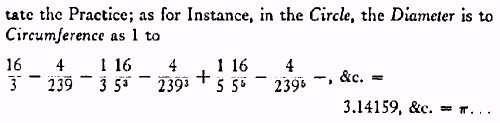
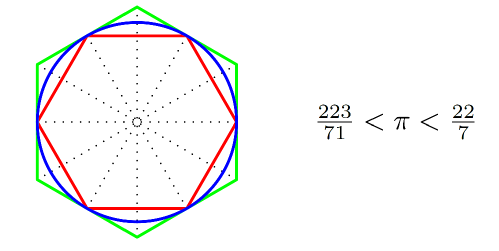
• $\ldots$ Archimedes al rond het jaar 250 vóór Christus benaderingen berekende voor het getal $\pi?$ Hij deed dit door te vertrekken van een cirkel met straal 1 en de halve omtrek te berekenen van ingeschreven en omgeschreven regelmatige veelhoeken met een toenemend aantal zijden (figuur links). Deze waarden geven begrenzingen naar onder en naar boven voor het getal $\pi$ (rechts). Het getal $\pi$ wordt daarom soms ook de constante van Archimedes genoemd. De benadering voor $\pi$ die Archimedes zo vond, heeft twee juiste decimalen. 

• $\ldots$  de oudste exacte uitdrukkingen waarmee je het getal $\pi$ kan berekenen, de volgende zijn?

• $\ldots$ Ludolph Van Ceulen (1540-1610), een Duits wiskundige, een groot deel van zijn leven spendeerde aan het (met de hand) uitrekenen van decimalen van $\pi$? Hij deed dit met de methode van Archimedes en geraakte tot aan de 35ste decimaal. Daarom wordt $\pi$ ook het Ludolfiaanse getal genoemd.
  Waarom met de hand? Omdat er in die tijd natuurlijk nog geen rekenapparatuur beschikbaar was. Het eerste (mechanische) rekentoestel dateert van 1623, dit jaar precies 400 jaar geleden:

• $\ldots$ William Shanks (1812-1882), een Brits amateur-wiskundige, het record van Van Ceulen ruimschoots verbeterde? Hij rekende 20 jaar lang met de hand aan de eerste 707
  decimalen van $\pi$ (1853). Hij had een vaste routine: 's morgens decimalen berekenen, 's namiddags de berekeningen checken. De formule die hij gebruikte, is de formule van Machin:
  $$
  \frac{\pi}{4} = 4 \cdot \mbox{Bgtg} \frac{1}{5} - \mbox{Bgtg} \frac{1}{239}
  $$
• $\ldots$ de 707 decimalen berekend door Shanks in 1937 op het plafond van één van de zalen van het Palais de la Découverte in Parijs werden geschilderd? Zie foto bovenaan. 
• $\ldots$ pas in 1946 werd ontdekt door D. F. Ferguson dat William Shanks een fout had gemaakt bij het 527ste cijfer na de komma, en dat de rest van zijn berekeningen dus ook waardeloos was? En die decimalen dus ook fout waren op het plafond van het Palais de la Découverte in Parijs? Ze werden in 1950 overschilderd. Diezelfde Ferguson was overigens de eerste die met behulp van een mechanische rekenmachine decimalen van $\pi$ berekende: 808 in 1947.
• $\ldots$ ondertussen $100\, 000\, 000 \, 000\, 000$ (dit spreek je uit als 100 biljoen) cijfers na de komma van het getal $\pi$ berekend zijn? (Met een computer natuurlijk, en betere formules!) Dit record werd op punt gezet in 2022 door Emma Haruka Iwao. De berekening heeft het equivalent van 158 dagen in beslag genomen.
• $\ldots$ John Venn (1834-1923) in 1888 wilde laten zien hoe random de decimalen van $\pi$ wel zijn, door voor de eerste 707 decimalen de cijfers 0-7 uit te zetten op een grafiek (zie figuur). Natuurlijk heeft hij zich gebaseerd op de foute berekening van Shanks!

• $\ldots$ ook het getal $\pi$-op-zijn-kop iets betekent in de wiskunde? Het is de notatie voor Belphegors priemgetal, een palindromisch getal enkel deelbaar door 1 en door zichzelf. Met in het midden 666 omgeven aan beide kanten door 13 nullen. Ongeluk gegarandeerd.

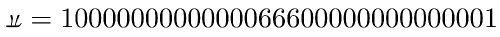
• $\ldots$ het getal
  $$
  \frac{\ln (640\,320^3+744)}{\sqrt{163}}
  $$
  om onduidelijke redenen tot op 30 cijfers na de komma gelijk is aan het getal $\pi$?
• $\ldots$ in de Amerikaanse staat Indiana de waarde van het getal $\pi$ in 1897 bijna bij wet is vastgelegd op 3.2? Dit laat ons toe om op 2 maart E. J. Goodwin-dag te vieren, naar de Amerikaanse dokter die dit wetsvoorstel toen heeft ingediend. 
• $\ldots$ het in Australië ook feest is op 31 augustus? Op die dag vieren ze daar $\pi$ down under day ($\frac{1}{\pi} = 0.3183...$).
• $\ldots$ je het getal $\pi$ regelmatig op onverwachte plaatsen tegenkomt, zoals op deze recente CD-cover? 

• $\ldots$  dat niemand weet wie de auteur is van deze limerick over de kwadratuur van de cirkel?
  Said the man about town, ‘I have a flair
  For squaring the circle, I swear.’
  But he found that the strain
  Was too great for his brain,
  So he’s gone back to circling the square.