Tijdens een eindeloze rit kijk je ongetwijfeld weleens naar het schermpje van de gps om te zien hoe lang het nog rijden is. Dat het toestel je dat kan vertellen, is te danken aan een knap staaltje technologie waarin heel wat wiskunde samenkomt. Wiskundige Ann Dooms (VUB) legt uit hoe die technologie werkt.
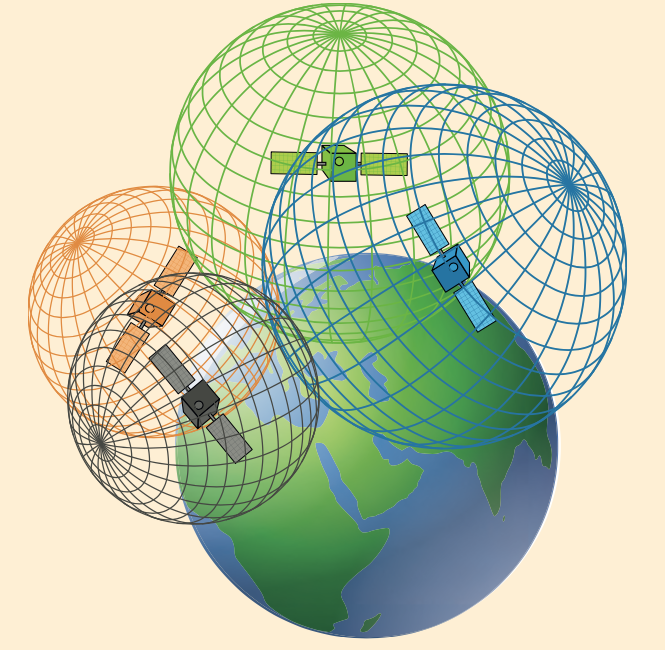
De gps in jouw auto of smartphone kan overal ter wereld worden gelokaliseerd, met dank aan 24 satellieten die 20.000 kilometer boven onze hoofden zweven en in 12 uur tijd rond de aarde draaien.
Doordat een satelliet een radiosignaal naar je toestel stuurt, kan het de afstand tot die satelliet bepalen. Het betekent dat jij je in de auto ergens in een bolvormige sfeer rondom de satelliet bevindt. Eén satelliet is niet voldoende om je exacte positie te kalibreren. Je afstand tot een tweede satelliet beperkt je mogelijke posities van een sfeer tot een cirkel (de doorsnede van de twee sferen van de satellieten). Een derde vernauwt je positie nog verder tot slechts twee mogelijke locaties. Met een vierde is je positie uniek bepaald. Ze kan nu worden gegeven in coördinaten uitgedrukt in een lengte- en breedtegraad. Wanneer je beweegt, zal je positie voortdurend opnieuw bepaald worden. Dat proces staat bekend als trilateratie.
Uit die data kunnen Google Maps, Waze en andere navigatieprogramma’s allerlei informatie halen over jouw route, zoals welke wegen je het best volgt en wat je geschatte aankomsttijd is. De programma’s gebruiken een kaart waarop alle wegen ter wereld staan, aangevuld met hun bijbehorende coördinaten en lengtes. Voor elke straat weet de software wat de snelheidslimiet is. Maar voor de berekening van de aankomsttijd moet ze ook rekening houden met de drukte op de weg. Daarom houdt ze ook bij hoe snel bestuurders in het verleden over een bepaalde weg reden en op welk moment van de dag ze dat deden.
Al die data worden verzameld op een graaf, een voorstelling van gegevens met hun onderlinge relaties. Hierop staan steden en kruispunten, zelfs huizen en hoe ze verbonden worden door wegen. Aan de verbindingen wordt dan extra informatie over tijd en lengte toegevoegd als een ‘gewicht’ – we spreken over een gewogen graaf.
Wanneer je een nieuwe bestemming ingeeft, kun je kiezen voor de snelste of kortste route. Het programma berekent dan welk traject daaraan voldoet. Daarvoor gebruikt het een algoritme ontwikkeld door Edsger Dijkstra (1930-2002) in 1956. Het geeft je een stapsgewijs recept voor hoe je het best doorheen de graaf loopt, zodat je van je start- tot je eindbestemming een lijst van wegen krijgt die samen het kleinste gewicht hebben in termen van tijd of afstand.
Grafentheorie ontstond trouwens uit een concreet routeprobleem. De wiskundige Leonhard Euler (17071783) bestudeerde in 1736 een vraag van enkele bewoners van het Duitse Königsberg (nu Kaliningrad in Rusland). De Pregel-rivier deelde de stad op in vier delen, waarvan twee eilanden. Die delen werden verbonden door in totaal zeven bruggen. De bewoners wilden door de stad kunnen wandelen en elke brug precies eenmaal oversteken om dan zo weer thuis aan te komen.
Euler maakte een abstracte voorstelling van de stad. Uiteindelijk doet het er namelijk niet toe waar de bruggen juist liggen – het draait om welke stadsdelen die bruggen verbinden. Zo werd de grafentheorie geboren. Hij bewees ermee dat het gevraagde tochtje onmogelijk is. Daarvoor zou je een even aantal verbindende bruggen moeten hebben. Inderdaad, telkens als je in een stadsdeel arriveert, moet je er met een ongebruikte brug opnieuw uit kunnen vertrekken. In gevallen waar zo’n wandeling wél mogelijk is, spreken we van een Eulercyclus. Misschien dat Google de optie Eulercyclus als extra functionaliteit kan inbouwen in Maps. Kan handig zijn, nu we met z’n allen het wandelen hebben herontdekt.