Enkele jaren geleden raakte ik gefascineerd door de elektrische eigenschappen van water. Goed een jaar geleden realiseerde ik me dat ik die enkel kon begrijpen door de elektrische eigenschappen van ijs te doorgronden (zie vorige blog). Ik had evenwel geluk, het werk in ijs was al gedaan. In de jaren 60 ontwikkelde Jaccard een allesomvattende theorie die beschreef hoe ladingen zich verplaatsen in ijs. Ik stond wel wat versteld. Ik heb tijdens mijn studies intensief vaste stoffen bestudeerd. Toch heeft niemand me toen uitgelegd hoe bijzonder de elektrische eigenschappen van ijs zijn. De meest voorkomende vaste stof op het aardoppervlak is te weinig gekend. 

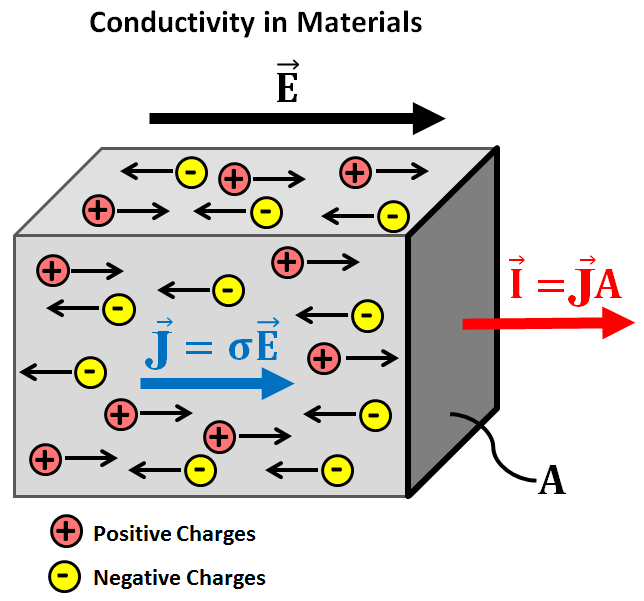
Jaccard had door dat er in ijs een sterke koppeling was tussen de oriëntatie van de watermoleculen en de beweging van de ladingsdragers en dit is best wel uitzonderlijk. In zo goed als alle andere vaste stoffen bewegen de ladingdragers (vb. elektronen, gaten, ionen, …) doorheen de structuur zonder die fundamenteel te veranderen (zie Fig. 1). Niet zo in ijs en we zullen in een volgende blog haarfijn uitleggen hoe dit in zijn werk gaat. Het thema van deze blog is evenwel … wiskunde. 

Jaccard slaagde erin om het verband tussen de oriëntatie van de watermoleculen en de beweging van de ladingen in ijs samen te vatten in enkele vergelijkingen (zie Fig. 2). Deze zijn bovendien nog eens vrij gemakkelijk analytisch op te lossen. Jaccard’s theorie was geboren en de overeenkomst met de experimentele resultaten was indrukwekkend. 

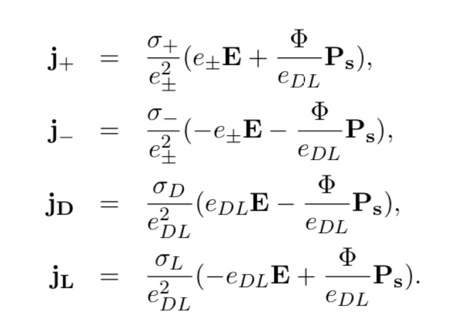
Van zodra fysici een samenhangende set vergelijkingen hebben, worden ze rustig en hebben ze het gevoel dat ze het systeem volledig begrijpen. Maar is dat wel zo? Jaccard zijn vergelijkingen kwamen natuurlijk niet uit de lucht vallen. Ze werden stap voor stap opgebouwd uit de vergelijkingen van Maxwell en een aantal veronderstellingen over de structuur van ijs. Het echte inzicht zit niet in de formules maar wel in hoe men tot deze formules is gekomen. En hier knelde het schoentje. In zijn eerste afleiding gebruikte Jaccard voor de hand liggende kinetische argumenten om de beweging van de ladingdragers in ijs te beschrijven. Maar hij kwam steeds een factor 2 te veel uit in de tweede termen van Fig. 2 (er stond dus 2 Phi in plaats van Phi). Hij raakte er niet aan uit en na enkele jaren zoeken, forceerde hij de zaak: hij verving zijn initiële kinetische afleiding door een veel abstractere afleiding (vanuit een aantal algemene thermodynamische eigenschappen van ijs) die wel de juiste uitkomst had. De nieuwe aanpak verklaarde evenwel niet waarom de kinematische aanpak niet werkte. Hier werd duidelijk een fundamenteel probleem verborgen. 

Jaccard’s formules werden snel succesvol en lieten toe om meerdere experimentele resultaten grondig te begrijpen. Dat ze niet zo gemakkelijk af te leiden zijn, werd al snel vergeten. Maar mij liet het probleem niet los. Ik wou deze vergelijkingen toepassen in de context van water, dus moest ik wel begrijpen hoe ze juist werden opgebouwd. Hoe kon ik anders de formules uitbreiden naar de interstitiële ijsstructuur van water (zie vorige blog). Ik begon dus opnieuw aan de afleiding waarop Jaccard was vast gelopen. 

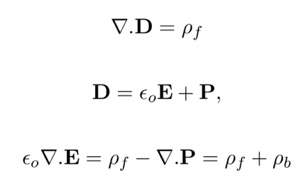
Ik ben Prof. Pauwels (mijn docent aan UGent) nog steeds dankbaar dat hij me een grondig inzicht in de theorie van het elektromagnetisme heeft meegegeven. Ik had al snel door dat die factor 2 niet de enigste zwakke schakel in de Jaccard's theorie was. Er was ook vrij slordig omgesprongen met het onderscheid tussen vrije en gebonden ladingen (voor de wetenschappers onder jullie zie Fig. 3). Door dit onderscheid consequent mee te nemen, kon ik de theorie op een veel eenvoudigere manier opbouwen en enkele fouten (zoals die factor 2) verbeteren (hier vind je een volledige beschrijving). 

De vergelijkingen waren dus wel af te leiden uit voor de hand liggende kinetische overwegingen. Die thermodynamische omweg was overbodig. Ik kon nu veel beter visualiseren hoe de beweging van de ladingdragers echt in elkaar zat (zie volgende blog) en maakte ook de wiskunde achter deze processen toegankelijker. Hierdoor was ik pas echt klaar om Jaccard’s theorie uit te breiden naar water. 

Dit verhaal wou ik even kwijt. Niet alleen omdat het mijn eerste echte succes was in een jarenlange zoektocht, maar ook omdat het veel zegt over wat echt inzicht (of 'deep understanding’) nu juist is. Ik zie het ook dikwijls bij mijn studenten. Ze denken dat ze iets begrijpen omdat ze de juiste formule kunnen opschrijven, maar ze ontbreken  een duidelijk beeld van het verhaal achter deze formules. Wat zijn de voorwaarden? Wat betekent elke grootheid nu weer? Wat is de invloed van die kwadratische factor?... Sommige handboeken fysica en vele papers zijn van hetzelfde bedje ziek. De vergelijkingen vliegen je rond de oren zonder voldoende aandacht voor hun betekenis. Moeilijke wiskundige afleidingen zijn een statussymbool geworden, iets in de zin van: 'Kijk eens hoe slim ik wel ben.’ Maar zit het echte inzicht niet verborgen in de eenvoudige afleidingen? Moeilijk is dan een synoniem voor: 'ik begrijp het nog net niet volledig'. 

Dit wil niet zeggen dat fysica geen formules nodig heeft. 'Het boek van de natuur is geschreven in de taal van de wiskunde’ zei Galilei volledig terecht, maar hij was tezelfdertijd ook de man die zijn wiskundige inzichten via fascinerende dialogen aan een groot publiek kon uitleggen (Fig.5). 

Nu het verhaal achter de formules van Jaccard duidelijk is, kunnen we in de volgende blog (Waarom is ijs een bijzondere halfgeleider?) met het echte werk beginnen. Hoe zit dat nu met de elektrische geleiding in ijs en wat maakt die zo speciaal? Dit wordt een blog voor de doorzetters, diegenen die echt diep willen gaan en hun inzicht in de materie verrijken. Ik beloof je dat ik geen wiskundige formules ga gebruiken.