Wiskundige Dirk Huylebrouck ontving een bijzondere brief van een Amerikaanse inmate: of hij eens naar zijn formule wilde kijken.
In zijn roman Aantekeningen uit het dodenhuis (1861/1862) stelt de Russische schrijver Fjodor Dostojevski dat de mate van beschaving in een samenleving kan worden beoordeeld door de gevangenissen binnen te gaan. Ik dacht aan die uitspraak toen ik onlangs een e-mail kreeg vanuit een Amerikaanse gevangenis. Ik had immers over de voor moord veroordeelde Christopher Havens geschreven in mijn boek Dark and Bright Mathematics, omdat hij een project mág leiden van wiskunde voor gevangenen. Mijn boek was hem ter ore gekomen, zelfs in de gevangenis dus. Als Amerikaanse gevangenissen wiskundig onderzoek toelaten, dan is het er niet zo erg gesteld als actiefilms het laten uitschijnen.
De vraag van de inmate was niet of ik een vijl kon opsturen verborgen in een stokbrood, maar wat ik vond van zijn formule:
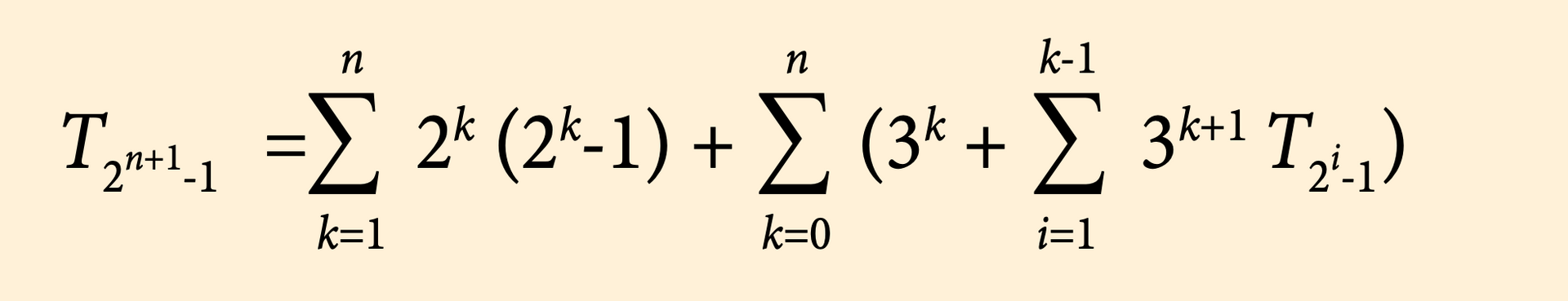
Hierin staat Tn voor het n-de Triangulaire getal, dat is de som 1+2+3+…n. Deze driehoeksgetallen danken hun naam aan het aantal cirkels die je op een rij van n cirkels kunt stapelen, zoals kanonskogels, maar dan in het vlak. De tekening toont waarom T1=1, T2=3, T3=6, T4=10, T5=15, T6=21, enz. (zie tekening 1) De oude Grieken stelden hiervoor al de algemene formule Tn = n(n+1)/2 op, maar anderen zouden haar nog enkele keren herontdekken. Menig schoolboek vertelt bijvoorbeeld hoe de jonge Carl Friedrich Gauss, die een van de belangrijkste wiskundigen zou worden, de getallen van 1 tot 100 optelde door er nog eens de getallen van 100 tot 1 bij op te tellen en zag dat dit steeds 101 is. Het dubbel van T100 is dus 100×(100+1).
Havens’ formule bouwt verder op een inzicht van Charles David Leach voor driehoeksgetallen van de machten van 2. Hij liet bij het driehoeksgetal T4 het middelste bolletje weg en bouwde de driehoeken in een zichzelf herhalende werkwijze op zoals in de tekening. Het aantal bolletjes op de snijpunten stemt nu overeen met de machten van … 3! (zie tekening 2)
Andere driehoeksgetallen vullen nu de ‘gaten’ in:
T4 =10 = 32 + 1 = 32 + T1 , T8=36 = 33 + 3.1 + 6 = 33 + 3. T1 + T3 , T16= 136 = 34+ 32.1 + 3.6 + 28 = 34+ 32.T1 + 3.T3 + T7, enz. Dat verklaart alvast het rechtergedeelte uit Havens’ formule.
Havens’ formule plaatst dergelijke driehoeken op elkaar en vult de overgebleven ruimtes op met machten van 2 (zie tekening 3). Ik heb hem geantwoord dat ze een mooi rekenkundig en geometrisch samenspel toont. Zou hij ze bedacht hebben door bolletjes op de muren van zijn cel te tekenen in plaats van streepjes?