Zie, 'k geef u thans, geleerden en leeken, ouden van dagen, frissche studenten ...

Zoals elk jaar rond deze tijd vieren we vandaag 14/3 $\pi$-dag. In Vlaanderen is het nog geen feestdag zoals in Amerika, maar ook wij mogen het vieren, vooral door vrienden, familieleden, collega's te trakteren op taart (pie dus)! Sinds 14 maart 2019 is $\pi$-dag dankzij UNESCO ook de internationale dag van de wiskunde!

We geven hier naar jaarlijkse traditie weer wat weetjes in verband met dat mysterieuze getal $\pi$!

Wist je al ...

• ... dat de Indische wiskundige Srinivasa Ramanujan (1887-1920) een heel speciale band had met het getal $\pi$? Hij liet een aantal notitieboeken na die gevuld waren met wiskundige formules. Het getal $ \pi $ staat op bijna elke pagina wel een paar keer. Aan hem wordt het volgende mnemomtechnisch middel toegeschreven om $\pi$ te onthouden:
  start met het getal 1234, wissel 2 maal 2 cijfers om, deel door 22 en en neem 2 maal de 2demachtswortel. Zo kom je uit op $$ \sqrt[4]{\frac{2143}{22}}$$ Reken nu zelf maar na hoe dicht bij het getal $\pi$ je hiermee komt.
   
• ... dat er in het afgelopen jaar geen record is gebroken voor wat betreft het berekenen van een groot aantal decimalen van het getal $\pi$? Wel worden er nog steeds nieuwe wiskundige technieken gevonden om $\pi$ te berekenen. De broers Chudnovsky hebben vele jaren geleden een oneindige som gevonden (overigens geïnspireerd door de sommen van diezelfde Ramanujan) die zodanig is dat elke extra term die je optelt bij de vorige zorgt voor 14 extra cijfers na de komma. Daarmee is jaren geleden zo'n $\pi$-record verwezenlijkt.
  Nu is er een nieuwe oneindige som waarbij elke extra term zorgt zomaar even voor 153 extra cijfers na de komma! (Dus de eerste term van die som geeft al 153 correcte cijfers, wat doet vermoeden dat de termen van die som eerder speciaal zijn, maar veel meer dan wat breuken, wortels en machten komt er niet in voor.)
   
• ... dat het naaldenexperiment van Buffon niet de enige vreemde methode is om een benadering te vinden voor het getal $\pi$? Botsingen tellen in een eenvoudig dynamisch systeem met twee bollen kan ook. Het verschil met Buffon is dat deze methode volledig deterministisch is, en dat je er $\pi$ mee kan berekenen tot op gelijk welke nauwkeurigheid. Hier zie je de opstelling:
   

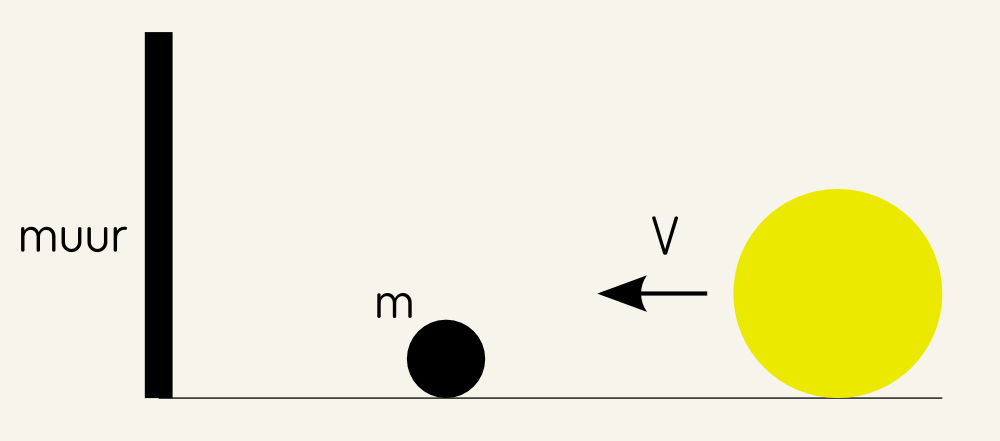
• Er wordt verondersteld dat de muur absoluut elastisch is. Laat de grote bol rollen in de richting van de kleine bol. Als de massa van de grote bol $100^N$ keer zo groot is als de massa van de kleine bol, dan is het aantal botsingen in dit systeem een getal met N+1 cijfers. De eerste N cijfers van dit getal zijn precies de eerste N decimalen van het getal $\pi$ (beginnend bij de 3).

• ... dat $\pi$ en de vierkantswortel van 7 onverwacht opduiken als je vertrekt van de oneindige som van de omgekeerden van de natuurlijke getallen, en dan de tekens in die som aanpast en bovendien de termen met noemer een veelvoud van 7 weglaat? Het lijkt er inderdaad op dat: $$ \frac{\pi}{\sqrt{7}} = 1 + \frac{1}{2} - \frac{1}{3} + \frac{1}{4} - \frac{1}{5} - \frac{1}{6} + \ldots $$ (je plaatst een minteken als de noemer een zevenvoud plus 3, plus 5 of plus 6 is). Bedankt Stijn om dit te melden! 
  En inderdaad, zoals verwacht wordt bij wiskunde: je kan ook bewijzen dat dit zo is.

• ... dat decimalen van $\pi$ van buiten leren de gewoonste zaak van de wereld wordt? In een recente aflevering van de reeks NCIS die vorige week werd uitgezonden, bekende Timothy McGee dat zijn eerste lief 1000 decimalen van $\pi$ uit het hoofd kon opzeggen!
  Er zijn tegenwoordig ook $\pi$-gerelateerde apps beschikbaar die je daarbij kunnen helpen indien je daar behoefte aan hebt.

• ... dat er sinds 2023 een bolvormig gebouw staat in Las Vegas? Je ziet het hier.
  In dat gebouw is er ook een $\pi$-muur:

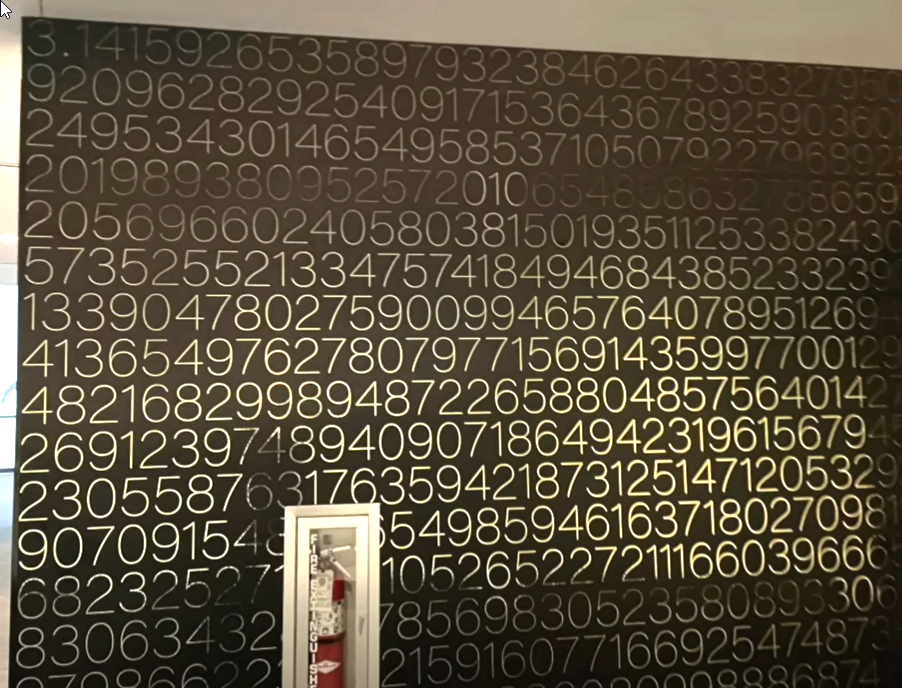
• ... dat $\pi$ voorkomt in verschillende afleveringen van de Simpsons? In een van die afleveringen, Lisa's Sax, zien we Homer en Marge een school bezoeken, waar ze twee wonderkinderen tegenkomen op het schoolplein, die hun eigen tekst hebben verzonnen voor een handjeklapliedje:

  Cross my heart and hope to die,
  Here’s the digits that make pi,
  3.14159265358979323846….

• ... dat het concept $\pi$-dag in feite gewoon iets dat uitgevonden is door de handelaars die hopen om zo op die dag meer wiskunde te kunnen verkopen?

Geniet van deze $\pi$-dag!