Zolang een netwerk groot genoeg is, zal er altijd structuur opduiken. Wiskundige Ann Dooms (VUB) legt de 'Ramseytheorie' uit aan de hand van zes willekeurige Facebook-profielen.
Wiskundigen houden van structuur. Er zijn er die specifieke structuren bestuderen, terwijl anderen verbanden proberen te leggen tussen verschillende structuren. Nog anderen gaan op zoek naar structuur waar er op het eerste gezicht geen is. In die laatste categorie hoort het werk van Frank P. Ramsey (1903-1930) thuis. De veel te vroeg gestorven Brit was er zich zelf mogelijk niet van bewust, maar zijn resultaten luidden een nieuw onderzoeksdomein in — een discipline die wiskundigen intussen al bijna honderd jaar zoet houdt.
Ramsey, van opleiding wiskundige, was van verschillende markten thuis: hij bewoog zich onder meer in de economie en filosofie. In het King’s College in Cambridge werkte hij samen met de bekende econoom John Maynard Keynes en de filosoof Ludwig Wittgenstein. Zijn publicaties gelden jaren later als invloedrijke werken van fundamenteel belang.
Al die opzienbarende verwezenlijkingen voeren de aandacht weg van één klein hulpresultaat in een wiskundig werk over logica. Het is een opmerkelijke uitkomst, die leidde tot de term ‘Ramseytheorie’. Wetenschappers spreken ook van de zoektocht naar orde in chaos.
Het idee valt het eenvoudigst te illustreren in termen van netwerken, zoals de sociale netwerken die je op Facebook vindt. Kies zes willekeurige personen op Facebook. Deze individuen kunnen bij voorbaat al onderling bevriend zijn of niet. Hoe dan ook heb je altijd ofwel een groepje van minstens drie personen die onderling bevriend zijn, ofwel een groepje van minstens drie personen die geen vrienden zijn.
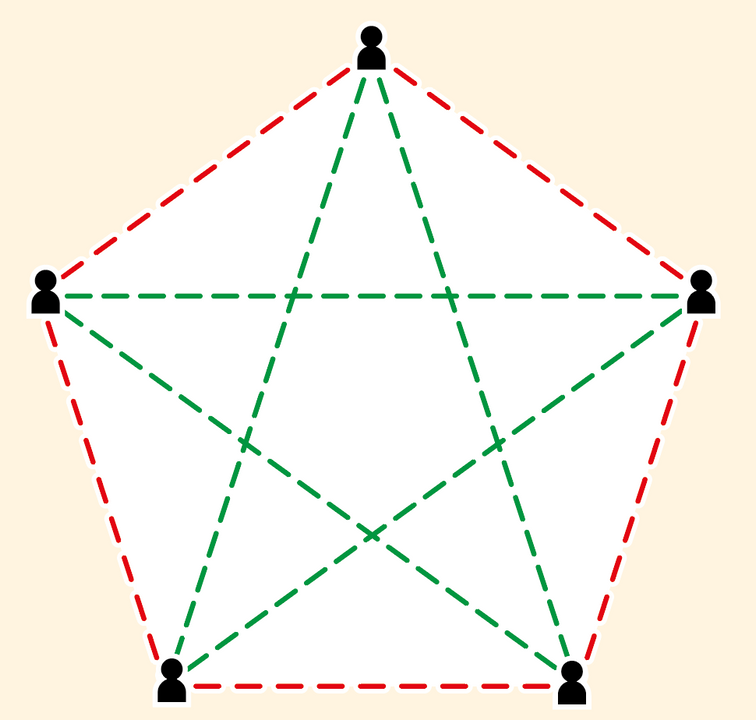
De groene lijnen wijzen naar vrienden, de rode naar onbekenden. Elke driehoek heeft ofwel twee rode lijnen en één groene ofwel één rode en twee groene.
In deze willekeurige selectie van zes profielen hebben we structuur gevonden: een groepje vrienden, of een groepje vreemden. Als we slechts vijf personen hadden gekozen, had dit fenomeen zich niet voorgedaan. Het achterliggende idee is dat zolang het netwerk groot genoeg is er altijd structuur zal opduiken. Dat hoeven niet altijd vrienden of vreemden te zijn. Het kan ook gaan om andere, complexere structuren.
De theorie heeft verregaande implicaties. In het voorbeeld met Facebook lijkt het logisch om op zoek te gaan naar grotere groepen vrienden of vreemden. Hoeveel profielen moeten we bijvoorbeeld kiezen om gegarandeerd een groepje van vier vrienden of vier vreemden aan te treffen? En wat als we dat voor eender welke grootte n zouden willen weten? Dat is exact hoe het Ramseygetal R(n) kan worden gedefinieerd. Het is het minimale aantal profielen dat we moeten kiezen om zeker een groep van n vrienden of n vreemden te vinden.
Zoals we hebben gezien is R(3) = 6. Met wat meer werk kan je aantonen dat R(4) = 18. Vanaf n = 5 wordt het al een heel ander verhaal, want tot op de dag van vandaag is de precieze waarde van R(5) onbekend. Om een idee te geven: in 1997 konden experts aantonen dat R(5) ≤ 49. Pas twintig jaar later kon men bewijzen dat R(5) ≤ 48. Omgekeerd weten we dat 43 ≤ R(5), en sommige experts zijn ervan overtuigd dat inderdaad R(5) = 43. Aan het huidige tempo kunnen we een sluitend bewijs verwachten in het jaar 2117.
'Als de aliens vragen naar de waarde van R(6), dan moeten we ze vernietigen' wiskundige Paul Erdős
Wetenschappelijke vooruitgang gaat natuurlijk steeds sneller. Hopelijk mogen we ons deze eeuw nog aan een oplossing verwachten. Misschien blijkt dit probleem zelfs een kolfje naar de hand te zijn voor de supercomputers van morgen. Al is dat minder waarschijnlijk dan je zou denken. Als je met brute kracht wil aantonen dat R(5) ≤ 43, dan zou de computer zo’n 10284 gevallen moeten doorlopen. Dat is een hoeveelheid waarbij het aantal atomen in het universum in het niet valt.
Of zoals Paul Erdős, één van de beste wiskundigen van de vorige eeuw, er volgens een collega het volgende over te zeggen had: ‘Stel je een vorm van buitenaards leven voor die vele malen geavanceerder is dan wij. De aliens landen op aarde en stellen ons voor de keuze: geef de precieze waarde van R(5) of onderga een mondiale uitroeiing. In dat geval moeten alle computers en alle wiskundigen ter wereld worden opgeëist en moeten ze samen proberen de waarde te vinden. Maar als de aliens in de plaats vragen naar de waarde van R(6), dan moeten we proberen de aliens te vernietigen.’




