Nooit meer file aan het damestoilet – technische bijlage

Deze bijlage hoort bij het artikel 'Nooit meer file aan het damestoilet'

Door Kurt Van Hautegem en Wouter Rogiest

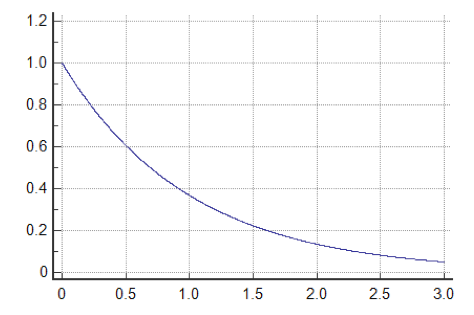
Zowel bij de formules van het Erlang-C wachtlijnmodel als de computersimulaties worden de tijden tussen de aankomsten (tussenaankomsttijd) verondersteld exponentieel verdeeld te zijn. De kansdichtheid van deze distributie wordt weergegeven in de figuur hiernaast. Bij het Erlang model is deze distributie een strikte voorwaarde, bij de simulatie een doordachte keuze. Het gebruik van deze distributie voor de willekeurig gekozen tussentijden resulteert immers in wat men een Poisson-aankomstproces noemt.

In de wachtlijntheorie wordt vaak een Poisson-proces gebruikt om aankomsten te modelleren aangezien dit een goede benadering biedt van de realiteit en bij theoretische berekeningen (Erlang-C model) vaak tot vereenvoudigd rekenwerk leidt. De reden dat zij de realiteit vaak goed benadert volgt uit de zogenoemde geheugenloze eigenschap van de exponentiële verdeling. Deze zorgt er voor dat de tijd verstreken sinds de vorige aankomst geen invloed heeft op de tijd tot de volgende aankomst. Of er nu reeds 10, 30 of 50 seconden geen aankomst is geweest, heeft geen invloed op de kans dat er een aankomst volgt in de komende seconde.

Deze eigenschap is een gevolg van de volledige onafhankelijkheid van de aankomsten bij een Poisson-proces en stemt overeen met de realiteit van een aankomstproces. Verder veronderstellen we steeds enkelvoudige aankomsten ook al gaan mannen en vooral vrouwen in de praktijk vaak in groepjes naar het toilet. Uit enkele bijkomende simulaties blijkt echter dat dit niet of nauwelijks invloed heeft op het verloop van de wachttijden in het door ons gekozen tijdsverloop.

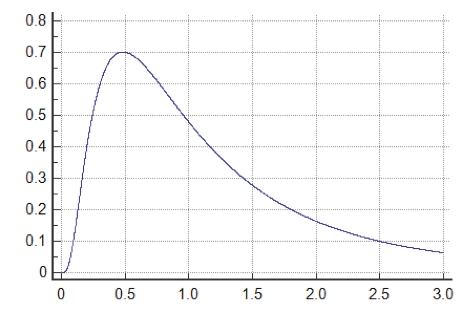
De tijd dat personen doorbrengen op het toilet (toilettijd) wordt bij het Erlang-C wachtlijn model tevens verondersteld exponentieel verdeeld te zijn. Waar dit een goede benadering is voor de doorschakeltijd van een call center is dit toch minder het geval voor de toilettijd in onze case.

Aangezien de simulaties hierin een extra vrijheid toelaten wordt de toilettijd dan ook gemodelleerd als een lognormale verdeling met variatiecoëfficiënt gelijk aan 1 in de simulaties. De kansdichtheid van deze distributie wordt weergegeven in de figuur hiernaast. In tegenstelling tot een normale verdeling vermijdt het gebruik van een lognormale verdeling op een natuurlijke manier dat negatieve toilettijden voorkomen. De variatiecoëfficiënt van 1 wordt vaak gebruikt in de literatuur. We veronderstellen ook dat mannen zowel op een hokje als urinoir terecht kunnen en dat hun toilettijd op beide dezelfde distributie volgt.

Een uitbreiding naar een geval waarbij een fractie van de mannen sowieso een toilethokje gebruikt en een daarbij horende langere toilettijd heeft is mogelijk maar hierbij is ons inziens het sop de kool niet waard. Deze uitbreiding vereist immers veel bijkomende parameters die geschat moeten worden en vraagt bij gescheiden toiletten om een bijkomende optimalisatie van de verhouding van het aantal hokjes en urinoirs voor mannen. Omdat deze fractie vaak eerder beperkt is zou de invloed hiervan op de uiteindelijke resultaten klein zijn en het vraagstuk dus nodeloos complex maken.

De verhouding van de nodige oppervlakte voor een urinoir en een hokje wordt ¾ verondersteld. Daarnaast veronderstellen we in de gesplitste lay-outs minstens twee toilethokjes voor de mannen. De totale oppervlakte ingenomen voor elke lay-out moet verder kleiner of gelijk zijn aan de oppervlakte ingenomen door 20 toilethokjes. Voor de gesplitste lay-outs geeft dit: (aantal vrouwentoiletten+2) x 1 + aantal urinoirs x 0.75 ≤ 20 en voor de gemengde lay-outs: aantal hokjes x 1 + aantal urinoirs x 0.75 ≤ 20. Door deze voorwaarde op te leggen gebruiken de verschillende lay-outs evenveel toiletoppervlakte en kunnen ze op een eerlijke manier vergeleken worden. De term "lay-out" verwijst overigens alleen naar de combinaties van aantallen toilethokjes (m/v/gemengd gebruik) en piscines; de precieze onderlinge schikking heeft geen impact op de resultaten.

We veronderstellen dat mensen de wachtrij niet verlaten. Indien mannen kunnen en moeten kiezen tussen twee wachtrijen (bij de gemengde lay-outs) gaan we ervan uit dat zij bij hun aankomst op intuïtieve wijze de kortste rij kiezen. Dit gebeurt in de simulatie op basis van de lengte van beide wachtrijen, de gemiddelde toilettijden en het aantal toiletten beschikbaar voor elke wachtrij.

Het systeem wordt gesimuleerd via een DES (Discrete Event Simulation). Een DES simuleert de werking van een systeem door te springen in de tijd van gebeurtenis naar gebeurtenis en bij elke gebeurtenis de toestand van het systeem te veranderen. De toestand is een aantal wiskundige variabelen die ondubbelzinnig de stand van zaken van het systeem beschrijven op het specifieke tijdstip. In het geval van gesplitste toiletten worden deze apart gesimuleerd en is de toestand van het systeem het aantal toiletten dat bezet is, samen met de lengte van de wachtrij. Bij een gemengd gebruik van toiletten met zowel hokjes als urinoirs zoals in lay-out 4 en 6 wordt er van twee types toiletten het aantal bezette en van twee wachtrijen de lengte bijgehouden. De gebeurtenissen in ons systeem zijn telkens de aankomst- en vertrektijdstippen van de toiletgangers. Deze tijdstippen worden bijgehouden in een agenda die chronologisch wordt afgewerkt. Bij elke gebeurtenis wordt ingelezen welk type gebeurtenis het is waarna de toestand op de juiste manier aangepast wordt (aantal vrije toiletten stijgt of daalt, de wachtrij groeit aan of neemt af). Daarnaast worden ook nieuwe gebeurtenissen gecreëerd. Zo zal bijvoorbeeld een aankomst automatisch de volgende aankomst creëren door een tussenaankomsttijd op te tellen bij het huidige tijdstip. Vervolgens wordt de huidige gebeurtenis uit deze vernieuwde agenda geschrapt en wordt de agenda opnieuw chronologisch gesorteerd. Zo wordt telkens opnieuw de eerste gebeurtenis uit de agenda verwerkt (toestand aanpassen, nieuwe gebeurtenissen creëren en agenda sorteren). Dit wordt herhaald tot een vooraf vastgelegd tijdstip bereikt wordt. De wachttijden worden onderweg bijgehouden en kunnen dan achteraf geïnterpreteerd worden.

Aangezien een DES niet elk moment simuleert maar slechts de momenten die er toe doen, is een DES typisch veel sneller dan een continue tijd-simulatie die hetzelfde simuleert. Deze laatste deelt de tijd op in zeer kleine intervallen die elk afzonderlijk geanalyseerd moeten worden, wat extra berekeningen vergt die op zich geen meerwaarde bieden. Om betrouwbare resultaten te bekomen wordt bovenstaande procedure om de agenda tot een bepaald tijdstip te verwerken 1000 maal herhaald en dit voor elke lay-out. Over dit grote aantal ‘runs’ worden de wachttijden van de klanten uitgemiddeld waardoor we betrouwbare resultaten krijgen van onze prestatiemaat. Het zijn deze uitgemiddelde wachttijden die getoond worden op de grafiek die het tijdsverloop van de gemiddelde wachttijd weergeeft.